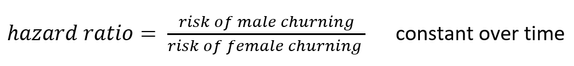Data Science
Machine learning & data science for beginners and experts alike.
Survival Analysis, Part 1: Introduction
Survival Analysis, Part 2: Key Models (You are here)
As we discussed in the previous section, survival analysis is different from standard regression or classification analysis. In this blog, we will introduce two of the most popular models used in survival analysis, namely the Kaplan-Meier (KM) model and the Cox Proportional Hazards (CPH) model.
The Kaplan-Meier (KM) Model
The KM model is a non-parametric method used to estimate the survival function. Ok, that’s a lot of jargon, so let’s try to break it down one by one. Non-parametric means that the KM model doesn’t make any assumptions about how our parameters are distributed, in other words, it offers flexibility. A survival function estimates the probability of an individual surviving past a given time point. Mathematically, it can be written as:
S(t) = P(T > t)
where T is the time to the event of interest and t is the given time point.
The survival function is a non-increasing function, meaning that as t increases, S(t) decreases. This is because as time passes, the probability of surviving is assumed to always decrease.
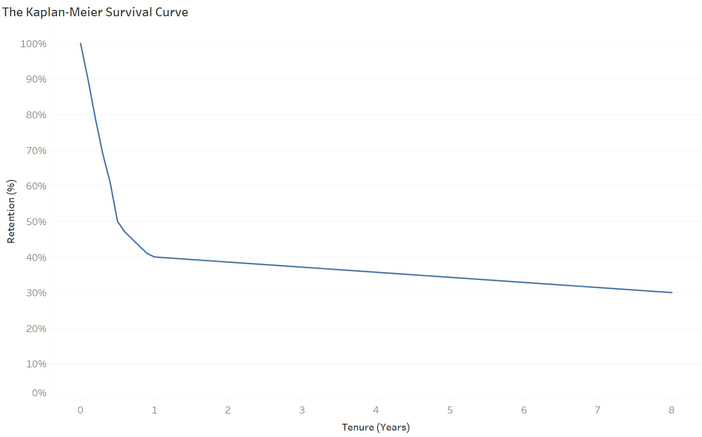
The KM model specifies a specific formula for estimating the survival function and is perhaps best explained visually through a graph (a survival curve, to be more precise). The survival curve shows the proportion of individuals who have not experienced the event of interest (in our case, customer churn) at each given time point.
One of the greatest advantages of the KM model is that it is easily interpretable. As the survival rate is cumulative, we can observe a significant decline in customer retention during the first year of the customer lifecycle. Specifically, the model predicts that less than 50% of customers are expected to remain with us after one year on average. From year one onward, there’s very little change in retention.
These are great insights that the KM model can reveal. For example, we can determine that the optimal time of intervention should occur well before a customer reaches the 2nd year of tenure. In practice, these findings should motivate further investigation of the data to understand why and what causes significant customer churn within the initial two years.
Pros:
- The KM model is easy to interpret and communicate.
- The Kaplan-Meier model can handle censored data, where an event has not occurred for some individuals at the time of analysis.
- Multiple groups can be shown on a KM curve to compare the effect of different interventions – for example, targeted marketing campaigns, a new type of medical treatment, or a switch to a new manufacturing process.
Cons:
- The Kaplan-Meier model does not account for the effects of covariates/confounders on the survival probability.
Assumptions:
- The Kaplan-Meier estimator assumes that the censoring is non-informative. In other words, the reason for censoring is unrelated to the outcome of interest. For example, in a clinical trial, censoring may occur when a patient withdraws from the study or the study ends. If the reason for censoring is related to the outcome of interest (e.g., patients with more severe disease are more likely to withdraw from the study), then the censoring may be informative, and the Kaplan-Meier estimator may provide biased estimates of the survival probability.
The KM model assumes a starting population of 100% for each plotted curve and that the survival probabilities are non-increasing over time.
The Cox Proportional Hazards (CPH) Model
The Cox Proportional Hazards Model is a semi-parametric model. It is non-parametric in the sense that it doesn’t make any assumptions regarding the distribution of the baseline hazard function. However, it is parametric because it assumes a functional form for the relationship between the hazard function and the covariates. More specifically, it assumes that the relative hazard of two individuals with different covariate values is constant over time.
Let’s go over some of the key concepts before we dive deeper:
- Hazard Function: This gives us the probability that our event of interest (e.g. churn) occurs at a specific time, given that the individual has survived up to that point.
- Covariates: In practice, past survival duration is not the only factor that can help us predict survival probability. There are other variables that co-occur (hence covariates) that also impact the probability of our event happening. For example, in our customer churn context, these additional covariates could include age, income, contract type, product type etc.
The CPH model does come with a strong assumption, yes you guessed it, it’s the proportional hazards assumption. This assumption maintains that a covariates hazard may change over time, but the hazard ratio remains constant over time. Assume we have a covariate called gender which contains males and females. The proportional hazards assumption says the risk of a male or female churning over time may change, but the ratio of the two is assumed to remain constant over time, that is:
The CPH model results in outputs that are quite similar to those of linear regression, and it allows you to explore the effect of different covariates on your event of interest. In general, the Cox Proportional Hazards Model can provide you with the following information:
- The variable coefficients and sign.
- The statistical significance of each variable.
- The hazard ratios.
These will become a lot clearer when we work through an example in Alteryx in the next blog, I promise!
Pros:
- The Cox model is designed to identify hazard ratios between groups, making it ideal for comparisons.
- The Cox model can handle censored data and can accommodate time-varying covariates.
- The model provides hazard ratios that represent the effect of a covariate on the hazard rate, which is easy to interpret and communicate.
- The model does not require any assumptions about the shape of the baseline hazard function, which makes it more flexible than parametric models.
Cons:
- The Cox model does not provide estimates of the baseline hazard function, which limits its ability to predict the absolute risk of the event of interest.
Assumptions:
- The Cox model assumes that the hazard function is proportional across different levels of the covariates. This assumption may not hold in some cases, leading to biased estimates of the hazard ratio.
- The model assumes that the censoring is non-informative.
