power regression to linear?

So, to be up front, i already have *a* solution to this problem.. and this more of a math question than it is an Alteryx question..

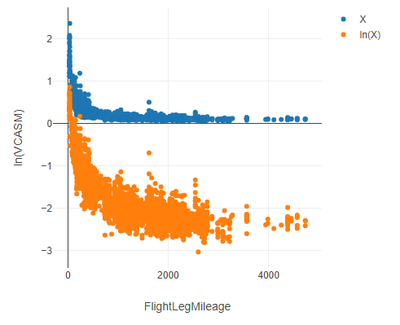
I have a data set (shown in blue) that very clearly follows a power curve. and the goal is to find a mathematical curve that best fits it

My current solution to use a python Curve_Fit function. It fits the data to the formula y = a*x^b.. This solution works well.. But since it's stepping through many iterations of 'a' and 'b' to find the best fit, it's kind of slow

After some googling, i have been led to believe that i should be able to mathematically transform the raw data into a linear trend.. then i can just do a linear regression on it.. but i cant figure out how to do that..

Are there any math whizzes out there that know if it's possible to transform this raw data from a power curve into a linear one?

New Workflow19.yxzp

Preparation

Accepted answers

Matthew

Got it! (kind of) my solution needs to be polished so i can build it into a macro, but i found the solution.. it isnt as elegant as having the actual power function (y = a*x^b), but at least with this method, i dont need a stepwise python script to find the power function by trial+error

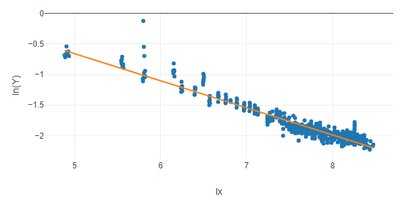
First i needed to take the natural log of both X and Y (Log(x), and Log(Y)). that transforms the data into a linear shape that i can calculate a line of best fit on

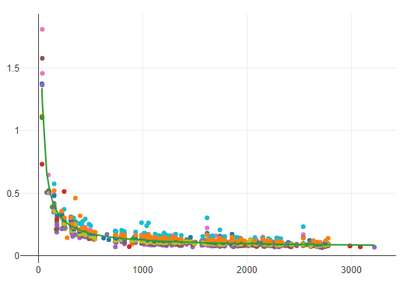
Then i plot all the values for that line of best fit

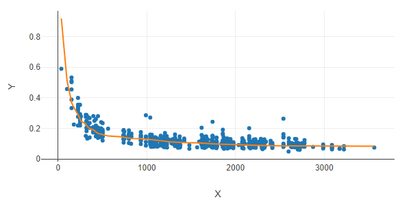
Then i can transform that line line back into normal numbers (e^LinReg), and plot it along side the original X and Y values

I feel like a wizard.

All comments

Matthew

First i needed to take the natural log of both X and Y (Log(x), and Log(Y)). that transforms the data into a linear shape that i can calculate a line of best fit on

Then i plot all the values for that line of best fit

Then i can transform that line line back into normal numbers (e^LinReg), and plot it along side the original X and Y values

I feel like a wizard.

ianwi

Very cool @Matthew!

Reminds me a little of the Kernel Trick from Support Vector Machines which I still think is awesome. Also a bit reminiscent of the Time Series transformations too.

Pretty nifty stuff - thanks for sharing what you've done here!

Matthew

@ianwi thanks for sharing those links!

i dont think a log transformation qualifies as a kernel trick, because i'm not introducing an additional dimension, but i see what you mean about it being similar because i'm manufacturing linearity!

Do you happen to have any resources for learning more about support vector machines or the kernel method?

ianwi

Hi @Matthew,

Glad you thought the Kernel Trick was interesting too!

Yes, we do have more resources on SVM in the Data Science Learning Path. Specifically it's in the Creating a Predictive Model Interactive Lesson. Loads of lessons in Academy on a wide variety of topics if you ever get curious...

Quick Links

This months top contributors

atcodedog05 19458

Qiu 15865

binu_acs 15708

MarqueeCrew 13708

apathetichell 13703