Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Re: Challenge #73: Plinko Probabilities
Challenge #73: Plinko Probabilities
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I modeled the board and then Monte Carlo'd until the pins wore off.
Like @patrick_digan, @jamielaird and @Kenda, I found the bounded model produces higher probabilities that token will end up in Bucket 1 or 5 if started in those columns


Because I modeled the board in the data input, I only needed 2 tools in the macro to simulate a run.

Dan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My solution.
Ummm wow, this one was exhausting for me.
Glad to know the posted solution looked up a pascal triangle because I spent a good half hour trying to manually count the paths to each space and gave up after a bit. Definitely not proud of my efficiency on this one. I walked away and came back to it on and off for 3 days researching different articles on Plinko probability.
So here it is, Didn't bother with the bonus, mostly cause i was burnt out by the time i got to the solution. Just glad to just check the box on this one and be done. :) No offense
I imagine you could add some interface tools on this approach to adjust the size of triangle you put through the calculation.
Cheers!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finally got it (I think...)
You input start column (in letters - A to E) and it gives you the output...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
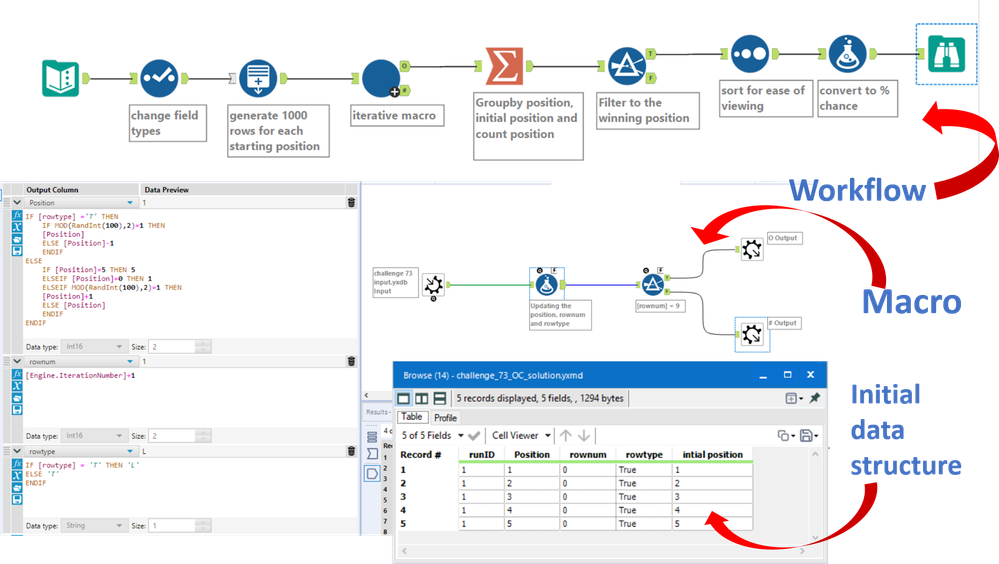
I went with an iterative macro which runs 1000 simulations for each starting position, and then works out the % of iterations which ended in the winning position. Worked with @George_Walker on this one :)
The formula updating the position in the macro uses whether a random integer is odd or even to decide whether to go left or right. We also need to appreciate that if a row has 6 blocks, (what I called a T(ight) row) and we are in the outer positions, we can only stay in the outer position. If we are in a row with 5 blocks (what I called a L(oose) row) we can always move left or right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi! Here my solution :)
Considering the game as an iteration of groups of two rows (a 4-pin row and a 5-pin row) plus a possible 5-pin row, I calculated the probabilities for a 2-row group and iterated as many times as groups existing; then, applying the posible 5-pin row probabilities.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
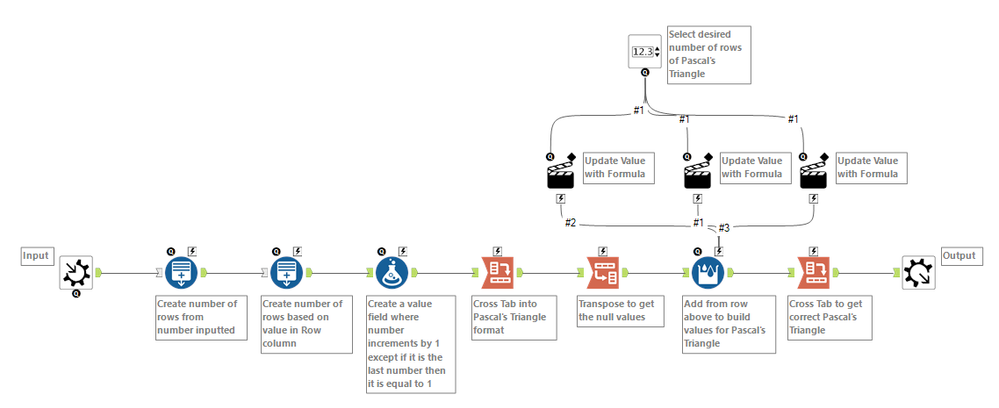
That took a while but eventually got there. First built a macro that builds Pascal's Triangle, then built a batch macro that calculates the chances of reaching each bin. The batch macro can be customised on the number of slots and number of rows.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's my solution to challenge 73!
I created an iterative macro that will allow you to decide the number of stages and tell you the probability of landing in any given position from any given space.
I define a stage as two sets of pegs - so every time the pegs line up to match the first row of pegs, that's a new stage.
I'm really happy with this as it took a lot of work to figure out how to iterate properly and figure out a cheeky way of passing multiple fields back in a single field (concat, pass back, seperate)!
-
Advanced
275 -
Apps
24 -
Basic
128 -
Calgary
1 -
Core
112 -
Data Analysis
171 -
Data Cleansing
4 -
Data Investigation
7 -
Data Parsing
9 -
Data Preparation
195 -
Developer
35 -
Difficult
71 -
Expert
14 -
Foundation
13 -
Interface
39 -
Intermediate
237 -
Join
206 -
Macros
53 -
Parse
138 -
Predictive
20 -
Predictive Analysis
12 -
Preparation
271 -
Reporting
53 -
Reporting and Visualization
17 -
Spatial
60 -
Spatial Analysis
49 -
Time Series
1 -
Transform
214
- « Previous
- Next »