Data Science
Machine learning & data science for beginners and experts alike.- Community
- :
- Community
- :
- Learn
- :
- Blogs
- :
- Data Science
- :
- Prescriptive Analytics: Unleash the Optimization T...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
Ever wonder what activities you could do in London with a time constraint? How about how to maximize the value of your fantasy football team on a budget? Join my session at Inspire to learn how prescriptive analytics and the Optimization Tool can help you find the best solution to your most pressing questions. I’ll go into more detail on the day, but to whet your appetite, here’s a little taster of what to expect…
The Types of Analytics
There are three (or four depending on who you ask) types of analytics. They build on one another and increase in both value and complexity. The types of analytics are:
- What has happened? This type of analytics describes what is already happening. This might include statistical measures such as the mean, median, standard deviation, correlation coefficient, etc.; Or it might be visualizing the data to glean insights. A lot of the data exploration can be done with Alteryx tools from the
Data Investigation tab.
- What will happen? After the initial exploratory data analysis, we can use the predictive tools from the
Predictive tab to predict what will happen. This could be forecasting the future, but more generally refers to making predictions on data points that don’t yet have an answer, like predicting engagement rates of an advertising campaign on new customers or identifying fraudulent transactions. The predictive models are probabilistic, and the outcomes are only the model’s best guess.
- What should I do? The third and most complex type of analytics is prescriptive analytics found in the
Prescriptive tab. One such type of prescriptive analysis is optimization, which will be the focus of this blog and my presentation at Inspire.
All types of analytics may be insightful and drive decisions, but prescriptive analytics can be used to find the best outcomes. This is optimization.
The Optimization Tool can be used wherever you are trying to maximize or minimize something subject to constraints. For example, in a business context you want to maximize profit, productivity, efficiency or minimize cost but with limitations on the resources or cost.
Doing Optimization
Let’s start with a straightforward example to see how this works.
Example 1 – Vitamin C
Let’s consider a simple example just to understand how the problem setup and Optimization tool works. Suppose you wanted to maximize your vitamin C intake from either apples or oranges. We google the nutrition content as:
If we ate x apples and y oranges then the total vitamin C would be,
As we are looking to maximize our vitamin C, we would eat as many apples and oranges as we could. In practice this would be as many as our stomach could handle, or as many as we could afford, or as many as we could carry home. These are the constraints we are faced with in real-world scenarios (and buying fruit). Let’s say that we only have a dollar, and that an apple is 10 cents and an orange is 30 cents. Then our constraint can be represented mathematically by the following inequality:
Now we have set our problem in a couple of mathematical statements – our objective function (the vitamin C that we want to get as much as possible) and our constraint (the thing that stops us buying infinite apples and oranges). The next step is to enter the values into input tools to feed into the Optimization Tool. There are a few ways to do this. One way is to have the following workflow:
We can see from the browse tool that the best way to spend our dollar is to buy 3 oranges and 1 apple to give us 161.7 mg of vitamin C. This makes sense: oranges have more vitamin C so we should buy more of them. We might even be able to come to this solution without using the Optimization Tool. But in this simple example we are only dealing with two variables (how many apples and oranges we should buy) and only one constraint (the cost). In other examples, there may be hundreds of variables and hundreds of constraints. In these cases, solving this by hand is all but impossible. In the next example, we consider a problem with more than two variables.
Example 2 – Knapsack Problem
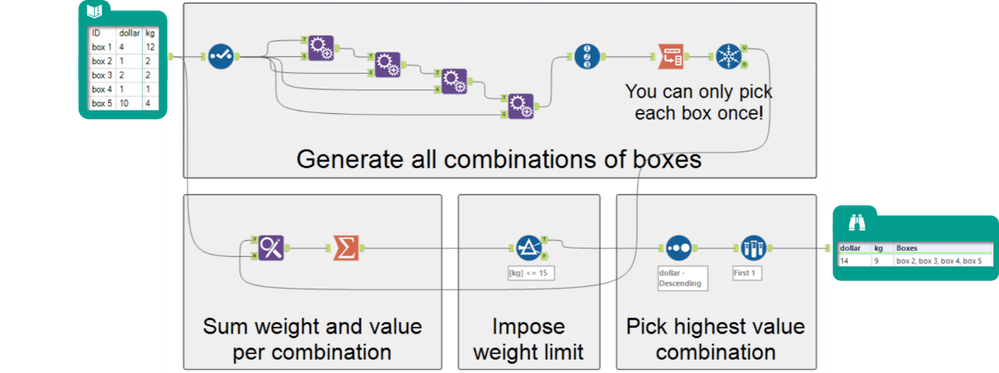
The knapsack problem makes things trickier because it introduces plenty more variables. The idea is you have a knapsack (or backpack) that you want to pack with the most valuable items without going over the weight limit. For example, say we have the following five boxes:
What’s the maximum value of all the boxes we can fit into our knapsack? In an ideal world we’d have all five boxes in our knapsack. But we also have a weight limit of 15kg. How would we go about solving this?
The mathematical formalization of this problem would be as follows:
Where x1, x2, x3, x4 and x5 are our variables. The values of these variables can only be 0 or 1 (unlike Example 1 where the variables could be any whole number) because we either select the box for the knapsack or we do not. In other words, the variables are binary.
And the constraint that the boxes cannot weigh more than 15 kg is:
It’s not immediately obvious which boxes we should include. We could use Alteryx to get every combination of boxes, filter out the combinations that exceed 15 kg, and then find the most valuable. This would be the brute force option and would look like:
This is fine; it still runs quickly. But as with Example 1, this is a simplified problem, in which we are optimizing for only 5 boxes. Imagine doing this for a warehouse instead of a knapsack! The number of Append Fields tools would grind your computer to a halt attempting to generate the combinations of thousands of items. This is where the Optimization Tool shines. The workflow with the Optimization Tool looks like this:
We would just add to the list in our Text Input tools should we want to include more boxes in our knapsack problem, and we don’t have to worry about generating ever more combinations. The Objective Value shown in the browse tool is the total value of our box 2, box 3, box 4 and box 5 – in this case, $14.
A variant of this problem is provided as one of the Alteryx Weekly Challenges here (the difference is that the Weekly Challenge requires you optimize by selecting 1 box, then 2 boxes, then 3 boxes, etc. whereas we want to find the overall optimized solution unconstrained by how many boxes we select and only constrained by weight limit).
Example 3 – Fantasy Football
What about something with some real practical value? The Fantasy Premier League provides a good example of the Optimization Problem using arguably the most-watched league in the world (although the following can be applied to similar fantasy leagues). The concept is to pick players that get points every week depending on how they perform. A good proxy for this is the ICT Index (which is kind of like a player rating).
The objective is to maximize the value of our players using the ICT Index. Formally we would write:
Note that in this example, the number of variables we wish to solve for has increased to the number of players playing in the English Premier League (over 300) for which finding every combination becomes very computationally expensive.
In Example 1 and Example 2 there was only one constraint. The rules of this game create multiple constraints. The main constraint is that the total value of your initial team must not exceed £100 million. There are also constraints such as selecting a squad of exactly 15 players (including 2 goalkeepers, 5 defenders, 5 midfielders and 3 forwards). Finally, no more than 3 players can be selected from any one Premier League team. These constraints can be written as:




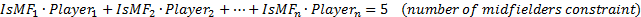
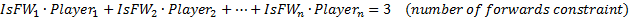




The cost constraint + total number of players constraint + the 3 position constraints + the 20 team constraints creates a total of 25 constraints that we need build into our model to feed into the Optimization Tool.
The set up looks like this:
And in less than a 3-second running time, we have our optimized team. The last step is of course making the necessary transfers:
And watching your team head straight to the top of your friend’s league.
Summary
Using the Optimization Tool can be a powerful way to increase the ROI in a work or social context. To use the tool, set up the objective function (the thing you want to maximize or minimize) and set up the constraints. It’s then a case of feeding these into the correct anchors, configuring the tool and running the workflow. Although this sounds straightforward, there are a few gotchas and tricks worth knowing to get the tool to run without error. If you’re interested in learning more about the Optimization Tool, I highly recommend you attend the Breakout Session at Inspire Europe 2019 where we will go into how you configure the Optimization Tool with plenty of examples like including maximizing time visiting London’s tourist attractions and maximizing the protein content in your diet. I look forward to seeing you there!
Author: Philip Mannering
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.