Analytics
News, events, thought leadership and more.- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
In my last blog post concerning the 2016 Presidential Election, I looked at how well the two-part model performed in correctly predicting the winner (a 96% success rate) of the Presidential election in each U.S. county. However, this was only one of two models that we created to forecast the election, the other is what is known as a "fundamentals" model, which is based on a very different approach than the two-part model. It turns out that combining the forecasts of these two models by taking a simple average of their predictions works better than either separately in predicting county-level results. This is actually a well-known phenomenon in the forecasting literature, but forecasting county-level results in the 2016 presidential election provides a concrete example of doing this.
“I start this final post on the 2016 election by introducing the ideas behind a fundamentals model, then present the county level fundamentals model we created, compare the ability of this model to predict county level results relative to the two-part model and an average of the predictions of the two models.”
I start this final post on the 2016 election by introducing the ideas behind a fundamentals model, then present the county level fundamentals model we created, compare the ability of this model to predict county level results relative to the two-part model and an average of the predictions of the two models. Finally, I briefly look at some important characteristics held in common by the small number of counties that the two models really missed the mark on in the election.
The Nature of Election Fundamentals Models
Beginning in the 1970s, both political scientists (such as Gerald Kramer and Edward Tufte) and economists (such as Ray Fair and George Stigler) began to develop statistical models that linked macroeconomic variables such as changes in unemployment rates and personal income on U.S. presidential election voting patterns. Initially, these models were focused on the national popular vote, and only examined the effect of macroeconomic factors (the economic "fundamentals"). Since then, other researchers have extended the approach by both including additional (non-macroeconomic) variables, and to predict U.S. presidential election voting at the sub-national (typically state) level. The target measure used in these models is the percentage of the Democratic and Republican vote that went to the Democratic candidate. This target measure is typically referred to as the “major party vote share.”
One model that has proven to work well is Alan Abramowitz's "Time-For-Change" model, which includes only three factors: the growth rate in the gross domestic product in the second quarter before a presidential election; the approval rating (as measured by Gallup's periodic presidential approval rating polls) of the incumbent president in mid- to late-June of the year of an election, and whether the same party has held the presidency for two or more terms. The GDP growth rate captures the underlying macroeconomic fundamentals; while the presidential approval rating captures the public’s judgment of the success of the party in power; and whether the incumbent party would remain in power for more than two terms captures the "time-for-change" in the model's name, and has been referred to as the "enthusiasm gap" in the 2016 election. Recent post-election analysis suggests that it was the enthusiasm gap that made the difference in this election.
A few researchers (such as the work of Hummel and Rothschild) have applied these models to sub-national presidential election returns. In addition to the variables included in the Time-for-Change model, variables that capture local area political preferences and trends in those preferences are included in the model, along with an attempt to capture candidate "home field advantage" effects. A natural candidate for capturing local political preferences is the Partisan Voting Index, or PVI.
Our County Level Fundamentals Model
The existing sub-national presidential election fundamentals models have been created at the state level, which is the natural level for these models since it allows for forecasting the Electoral College outcome. However, our interest is making predictions for lower level geographic areas, and the lowest level geography where the needed data is reported is at the county level. Consequently, we developed a fundamentals model at that level back in July of last year. All the data needed to make forecasts for the 2016 presidential election came available on August 1st, and we made the predictions from the fundamentals models on that date (over three months before the actual election). The data used to create the model is time series in nature, with the predictors included in the model (the choice of which was strongly influenced by the work of Hummel and Rothschild) being:
- The approval of the sitting president on or near June 15 the year of the election (the data is taken from Gallop polls)
- The difference in the GDP growth rate between the second quarter of the year prior to the election and the second quarter of the election year
- Whether the incumbent party has held the White House for eight years or more
- The PVI (calculated using county level returns data from the 1964 to 2008 elections) and a measure designed to capture the trend in the PVI for a county
- Whether the county is in the home state of the candidate and the state has a population under 4 million, and whether the county is the home state of a candidate in the prior election, and has a population under 4 million
- Whether the county is in a southern state and it is either the 1976 or 1980 election
The first three of these predictors are the measures used in the Time-for-Change model, while the PVI based measures capture county level partisanship effects and the expected trend in those effects. One thing that may be surprising is that to calculate the PVI we need data from as far back as the 1964 election. The reason is that the PVI is calculated using the prior two presidential elections, so the relevant value of the PVI in a county in 1972 is calculated based on returns data from the 1964 and 1968 elections. The last of the predictors are designed to capture "home field advantage" effects, and are also used in Hummel and Rothschild's state-level model. There is evidence that presidential candidates receive a benefit in their home state, if that state is not an extremely large state, for that election. This has an impact in that year's election, but will also tend to (artificially) boost up the PVI for that candidate's party in the following election (it also will boost the PVI in the subsequent election, but the effect in that election is much smaller due to the much greater, 75%, weight given to the most recent election in the PVI calculation we use). As a result, the combination of the two predictors addresses this situation. The southern state indicator for the 1976 and 1980 elections corresponds to the two elections in which Jimmy Carter of Georgia ran for the presidency.
“To create the model, we used a training/test approach in which we created models using the Linear Regression, Forest Model, Boosted Model, and Neural Network tools in Alteryx (examining different hyper-parameter values for the last three) in the training set, and compared their ability to predict new data in the test set.”
To create the model, we used a training/test approach in which we created models using the Linear Regression, Forest Model, Boosted Model, and Neural Network tools in Alteryx (examining different hyper-parameter values for the last three) in the training set, and compared their ability to predict new data in the test set. The model with the highest predictive accuracy in the test set is a Boosted Model with three-way interactions. This model configuration was re-estimated using the full data set to create the final forecasts. By far the most important variable in the model is the PVI, following this are the three variables from the Time-for-Change model (approval rating of the current president, the GDP growth rate, and whether the incumbent party has held the presidency for two or more terms) and the indicator of being a southern state in the 1976 election. The remaining variables had minimum impact.
Comparing Model Performance in Predicting County Level 2016 Election Results
Overall, the county level model does fairly well with an overall accuracy rate of nearly 95% (compared to just over 96% for the two-part model that backed our Presidential Election App) and has a correlation between the fitted and actual values of just under 0.95, nearly identical to the two-part model. Interestingly, the overall accuracy is higher for a simple average of the two models than each model individually, while the correlation between the fitted and actual values for the prediction average is over 0.97.
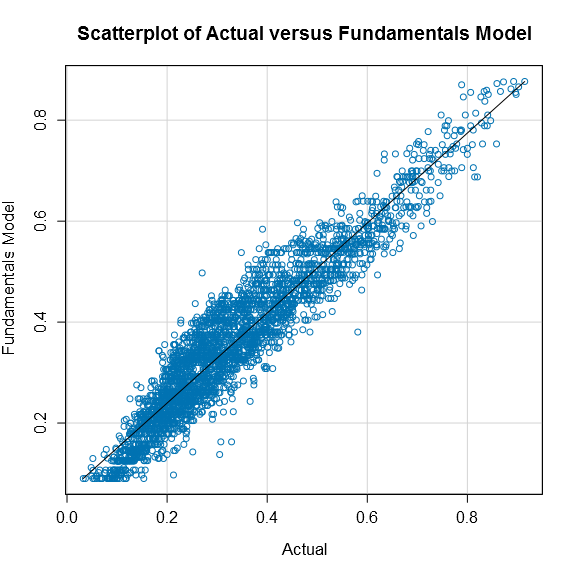
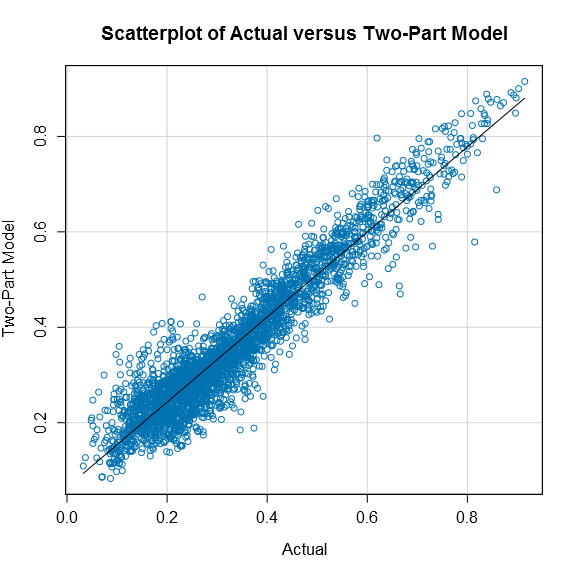
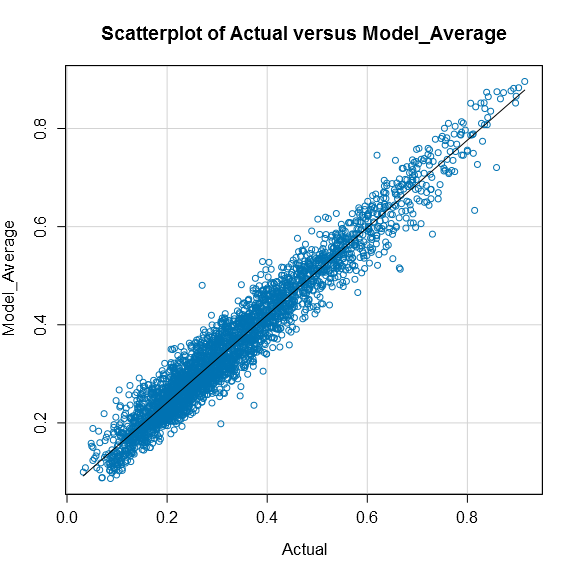
To provide a more complete comparison of the results of the different models, Figures 1 to 3 provide the plot of fitted versus actual values for the fundamentals model, the two-part model, and the average of the two models for the 2016 election, while Tables 1 to 3 provide a confusion matrix for each of the three sets of predictions. In addition, Table 4 provides other common model comparison metrics such as the mean absolute deviation (or MAD) and the mean absolute percentage error (or MAPE) for the 2016 election results.
Figure 1
Figure 2
Figure 3
All three figures indicate a very good fit between the fitted and actual values for the 2016 election. However, both the fundamentals and two-part models have areas of the plot that are not ideal with respect to their symmetry around the solid line. However, the fitted values obtained from averaging the predictions of the two models is much smoother and symmetric around the line.
| Actual | ||
| Fundamentals Model | Democratic | Republican |
| Democratic | 423 | 106 |
| Republican | 63 | 2519 |
Table 1
| Actual | ||
| Two-Part Model | Democratic | Republican |
| Democratic | 457 | 91 |
| Republican | 29 | 2534 |
Table 2
| Actual | ||
| Model Average | Democratic | Republican |
| Democratic | 461 | 88 |
| Republican | 25 | 2537 |
Table 3
The confusion matrix for each of the three models is actually very good, but the accuracy of the two-part model is better than the fundamentals model for both Clinton and Trump. Comparing Table 3 to Tables 1 and 2 reveals that the average of the two models is more accurate for both candidates than either model alone.
| Metric | Two-Part Model | Fundamentals Model | Model Average |
| Overall Accuracy | 0.9614 | 0.9457 | 0.9637 |
| Clinton Accuracy | 0.9403 | 0.8704 | 0.9486 |
| Trump Accuracy | 0.9653 | 0.9596 | 0.9665 |
| Correlation | 0.9497 | 0.9465 | 0.9717 |
| RMSE | 0.0579 | 0.0576 | 0.0473 |
| MAD | 0.0451 | 0.0446 | 0.0378 |
| MAPE | 20.13 | 16.54 | 15.94 |
Table 4
In terms of the other common metrics used to compare forecasts shown in Table 4, the fundamentals model actually slightly outperforms the two-part model with respect to root mean square error, mean absolute deviation, and mean absolute percentage error. However, averaging the predictions of the two models does better than either model alone on all the comparison metrics. The average error is 3.8 percentage points when the average of the predictions is used compared to about 4.5 percentage points when either model is used individually.
“Making predictions based on averaging other predictions is likely to perform better than any of the individual predictions when the predictions rely on different underlying information, and use different modeling approaches, which describes the current situation perfectly.”
While the fact that taking a simple average of the predictions of the two different models may be surprising, as pointed out in the introduction of this post, it is a well-known phenomenon in the forecasting literature. Making predictions based on averaging other predictions is likely to perform better than any of the individual predictions when the predictions rely on different underlying information, and use different modeling approaches, which describes the current situation perfectly.
The fundamentals model uses data from past actual election returns to predict future elections at the county level, while the two-part model makes use of pre-election polling data to predict individual voter behavior, and then aggregates those propensities across voters. The difference in data and modeling approaches likely means that the two forecasts are taking into consideration different aspects of the process. In particular, the polling data likely did not adequately capture the "enthusiasm gap" seen in this election, while it is explicitly captured in the "Time-for-Change" component of the fundamentals model. Specific aspects of the 2016 election, such as the low levels of popularity of the two major party candidates, cannot be accounted for by the fundamentals model, put are captured in the pre-election polling data. The average of the two different predictions allows the different aspects captured by the different predictions to be combined together, resulting in predictions that are more accurate on average.
A Brief Examination of Counties Where All the Models Went Wrong
In this section we look at some of the characteristics of counties where there were major surprises in the election results. The most important predictor in both the two-part and fundamentals model that were built is the Partisan Voting Index, as a result, we also include this factor directly as one of the criteria we use to define a “surprise.” A surprise for the Democrats is defined to be a county where the PVI was D+5 or higher, was predicted by all models to go to Clinton, but actually voted for Trump. Similarly, a surprise for the Republicans is defined to a county where the PVI was R+5 or higher, was predicted by all models to go to Trump, but actually voted for Clinton. In total, there were 17 counties that constituted an unpleasant surprise for the Democrats, and only a single count that was an unpleasant surprise for the Republicans (Cobb County, Georgia). It is important to note that only 18 out of the 3111 counties (less than one percent) fall into the “surprise” category as we have defined it. In Table 5 we present more detailed information on the counties that were unpleasant surprises for the Democrats, along with information concerning the population density of the county, the change in the county’s population between 2010 and 2015, and the change in net migration (which measures the extent to which people are moving into the county versus moving out of the county). In the table, the counties are ordered based on the size of the prediction error (based on the average of the two model predictions), with the county with the largest error listed first.
| County | State | PVI | Clinton Major Party Vote Share | Two-Party Model Clinton Major Party Vote Share | Fundamentals Model Clinton Major Party Vote Share | Forecast Average Clinton Major Party Vote Share | Population Density | Percent Population Change 2010 to 2015 | Percent Net Migration 2010 to 2015 |
| Essex | VT | D+5 | 40.4 | 51.7 | 53.8 | 52.7 | 9.5 | -2.2 | -2.1 |
| Franklin | NY | D+10 | 46.1 | 55.6 | 59.7 | 57.6 | 31.7 | -1.9 | -2.5 |
| Ziebach | SD | D+7 | 48.9 | 61.8 | 56.4 | 59.1 | 1.5 | -0.8 | -4.8 |
| Corson | SD | D+5 | 47.6 | 59.1 | 53.8 | 56.4 | 1.6 | 3.2 | -2.1 |
| Franklin | ME | D+7 | 47.0 | 55.2 | 55.3 | 55.2 | 18.2 | -2.4 | -1.7 |
| Coos | NH | D+7 | 45.2 | 51.1 | 55.3 | 53.2 | 18.1 | -5.4 | -3.0 |
| Mower | MN | D+9 | 45.8 | 50.9 | 56.6 | 53.7 | 55.5 | -0.2 | -1.9 |
| Crawford | WI | D+9 | 47.1 | 52.8 | 57.3 | 55.1 | 29.4 | -1.5 | -1.2 |
| Clinton | IA | D+9 | 47.3 | 51.6 | 58.4 | 55.0 | 70.5 | -2.7 | -3.1 |
| Trumbull | OH | D+9 | 46.7 | 51.4 | 56.6 | 54.0 | 337.8 | -2.9 | -2.0 |
| Kennebec | ME | D+5 | 48.0 | 54.5 | 53.8 | 54.1 | 140.5 | -1.7 | -0.7 |
| Blaine | MT | D+6 | 48.5 | 54.6 | 54.6 | 54.6 | 1.6 | 1.3 | -1.8 |
| Kent | RI | D+7 | 49.6 | 55.2 | 55.3 | 55.3 | 980.1 | -0.8 | -0.4 |
| Robeson | NC | D+6 | 47.5 | 52.1 | 53.8 | 53.0 | 143.8 | -0.1 | -2.4 |
| Essex | NY | D+6 | 48.2 | 50.4 | 55.7 | 53.0 | 21.8 | -2.1 | -1.2 |
| Sullivan | NH | D+5 | 48.6 | 53.0 | 53.8 | 53.4 | 80.6 | -1.8 | -1.2 |
| Kenosha | WI | D+5 | 49.8 | 52.2 | 53.8 | 53.0 | 617.1 | 1.1 | -0.8 |
Table 5
An examination of the table reveals several things. First, most of the counties that were an unpleasant surprise for the Democrats were rural counties (based on population density), with many located in New England, Upstate New York, and the Upper Midwest. In addition, 14 of the 17 counties experienced a declining population between 2010 and 2015, and all experienced a negative net migration rate (more people are moving out of these counties then are moving into them). The typical county in this group is a rural county facing a declining population, and likely declining economic circumstances. In contrast, Cobb County, Georgia (the only unpleasant surprise for the Republicans, which had a PVI of R+8, but voted for Clinton) is more urban (its population density is over 2000 people per square mile, double that of the most dense of the 17 surprise counties for the Democrats), its population is growing, and it is experiencing positive net migration.
These results are consistent with much of the analysis that has been conducted since the election on the urban vs rural split in this election, and the support of voters who are feeling left behind economically. What is somewhat surprising is that while the analysis of the phenomenon in the media has focused on the so called “Rust Belt” of Pennsylvania, Ohio, and the Upper Midwest, these factors also are at play in Upstate New York and New England.
As I write this the inauguration of the Donald J. Trump as the 45th president of the United States has occurred. Appropriately, our analysis of the election (both before and after) is fairly complete. I hope that readers in the Alteryx Community found this series of blog posts on the 2016 presidential election interesting, and I thank you for reading the posts in the series.

Chief Scientist
Dr. Dan Putler is the Chief Scientist at Alteryx, where he is responsible for developing and implementing the product road map for predictive analytics. He has over 30 years of experience in developing predictive analytics models for companies and organizations that cover a large number of industry verticals, ranging from the performing arts to B2B financial services. He is co-author of the book, “Customer and Business Analytics: Applied Data Mining for Business Decision Making Using R”, which is published by Chapman and Hall/CRC Press. Prior to joining Alteryx, Dan was a professor of marketing and marketing research at the University of British Columbia's Sauder School of Business and Purdue University’s Krannert School of Management.
Dr. Dan Putler is the Chief Scientist at Alteryx, where he is responsible for developing and implementing the product road map for predictive analytics. He has over 30 years of experience in developing predictive analytics models for companies and organizations that cover a large number of industry verticals, ranging from the performing arts to B2B financial services. He is co-author of the book, “Customer and Business Analytics: Applied Data Mining for Business Decision Making Using R”, which is published by Chapman and Hall/CRC Press. Prior to joining Alteryx, Dan was a professor of marketing and marketing research at the University of British Columbia's Sauder School of Business and Purdue University’s Krannert School of Management.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.