FIFO Calculation with multiple products

[AustinLeung]

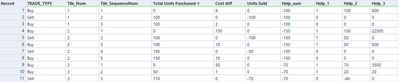
I am trying to calculate the cost of sales under First-in-first-out method. The cost could be calculated by excel, which is in column N in the "Results" file. However, I am not sure how I could use Alteryx to do the same thing.

Any help is much appreciated. Thanks in advance.

Cheers,

Austin

[AustinLeung]

Hi @grossal,

Sorry that I miss the negative sign in my last reply.

The formula in the excel is =SUMPRODUCT(--(-SUM($L$3:L4)>I$3:I4),-SUM($L$3:L4)-$I$3:I4,K$3:K4)-SUM($M$3:M3)

So the first part should be as below.

-SUM($L$3:L4) > I3 ->   100 > 0     -> True -> 1

-SUM($L$3:L4) > I4 ->   100 > 100 -> False -> 0

Apologies for the confusion

[AustinLeung]

The logic of the last formula may not seem intuitive. I would definitely love to see other approach that would be more straightforward to get the results.

I try to divide the formula into different parts below. You may also use "Evaluate formula" function in excel to simplify the formula as well.

Let's take the formula in cell M4 as an example:

=SUMPRODUCT(--(-SUM($L$3:L4)>$I$3:I4),-SUM($L$3:L4)-$I$3:I4,$K$3:K4)-SUM($M$3:M3)

1st part: --(-SUM($L$3:L4)>$I$3:I4)

= {IF -SUM($L$3:L4) > I3, THEN = 1, ELSE 0; IF -SUM($L$3:L4) > I4, THEN = 1, ELSE 0}

= {1;0}

2nd part: -SUM($L$3:L4)-$I$3:I4,$K$3:K4

= {-SUM($L$3:L4) - I3 ; -SUM($L$3:L4) - I4} , {$K$3 ; K4}

= {100-0 ; 100-100}, {8 ; 0}

= {100 ; 0} , {8 ; 0}

3rd part: -SUM($M$3:M3)

= 0

So, adding all parts will equal to SUMPRODUCT( {1;0} , {100;0} , {8;0} ) - 0

= (1*100*8 + 0*0*0) - 0

= 800

Using the same logic, the formula in cell M9 =SUMPRODUCT(--(-SUM($L$6:L9)>$I$6:I9),-SUM($L$6:L9)-$I$6:I9,$K$6:K9)-SUM($M$6:M8)

=SUMPRODUCT ( {1;1;1;0} , {150;50;50;0} , {150;0;10;0} ) - SUM(M6:M8)

= ( 1*150*150 + 1*50*0 + 1*50*10 + 0*0*0 ) - 15000

= 8000

The logic is to calculate the cumulative total cost of sales starting from the beginning by SUMPRODUCT(--(-SUM($L$6:L9)>$I$6:I9),-SUM($L$6:L9)-$I$6:I9,$K$6:K9) and subtract the previous cost of sales up to the last transaction with -SUM($M$6:M8). So, the remaining balance would be the non-cumulative cost of sales for that particular transaction. Hope this is clearer.

[AustinLeung]

The logic of the last formula may not seem intuitive. I would definitely love to see other approach that would be more straightforward to get the results.

I try to divide the formula into different parts below. You may also use "Evaluate formula" function in excel to simplify the formula as well.

Let's take the formula in cell M4 as an example:

=SUMPRODUCT(--(-SUM($L$3:L4)>$I$3:I4),-SUM($L$3:L4)-$I$3:I4,$K$3:K4)-SUM($M$3:M3)

1st part: --(-SUM($L$3:L4)>$I$3:I4)

= {IF -SUM($L$3:L4) > I3, THEN = 1, ELSE 0; IF -SUM($L$3:L4) > I4, THEN = 1, ELSE 0}

= {1;0}

2nd part: -SUM($L$3:L4)-$I$3:I4,$K$3:K4

= {-SUM($L$3:L4) - I3 ; -SUM($L$3:L4) - I4} , {$K$3 ; K4}

= {100-0 ; 100-100}, {8 ; 0}

= {100 ; 0} , {8 ; 0}

3rd part: -SUM($M$3:M3)

= 0

So, adding all parts will equal to SUMPRODUCT( {1;0} , {100;0} , {8;0} ) - 0

= (1*100*8 + 0*0*0) - 0

= 800

Using the same logic, the formula in cell M9 =SUMPRODUCT(--(-SUM($L$6:L9)>$I$6:I9),-SUM($L$6:L9)-$I$6:I9,$K$6:K9)-SUM($M$6:M8)

= SUMPRODUCT ( {1;1;1;0} , {150;50;50;0} , {150;0;10;0} ) - SUM(M6:M8)

= ( 1*150*150 + 1*50*0 + 1*50*10 + 0*0*0 ) - 15000

= 8000

The logic is to calculate the cumulative total cost of sales starting from the beginning by SUMPRODUCT(--(-SUM($L$6:L9)>$I$6:I9),-SUM($L$6:L9)-$I$6:I9,$K$6:K9) and subtract the previous cost of sales up to the last transaction with -SUM($M$6:M8). So, the remaining balance would be the non-cumulative cost of sales for that particular transaction. Hope this is clearer.

[AustinLeung]

My earlier reply got deleted after editing. Trying to repost below

The logic of the last formula may not seem intuitive. I would definitely love to see other approach that would be more straightforward to get the results.

I try to divide the formula into different parts below. You may also use "Evaluate formula" function in excel to simplify the formula as well.

Let's take the formula in cell M4 as an example:

=SUMPRODUCT(--(-SUM($L$3:L4)>$I$3:I4),-SUM($L$3:L4)-$I$3:I4,$K$3:K4)-SUM($M$3:M3)

1st part: --(-SUM($L$3:L4)>$I$3:I4)

= {IF -SUM($L$3:L4) > I3, THEN = 1, ELSE 0; IF -SUM($L$3:L4) > I4, THEN = 1, ELSE 0}

= {1;0}

2nd part: -SUM($L$3:L4)-$I$3:I4,$K$3:K4

= {-SUM($L$3:L4) - I3 ; -SUM($L$3:L4) - I4} , {$K$3 ; K4}

= {100-0 ; 100-100}, {8 ; 0}

= {100 ; 0} , {8 ; 0}

3rd part: -SUM($M$3:M3)

= 0

So, adding all parts will equal to SUMPRODUCT( {1;0} , {100;0} , {8;0} ) - 0

= (1*100*8 + 0*0*0) - 0

= 800

Using the same logic, the formula in cell M9 =SUMPRODUCT(--(-SUM($L$6:L9)>$I$6:I9),-SUM($L$6:L9)-$I$6:I9,$K$6:K9)-SUM($M$6:M8)

= SUMPRODUCT ( {1;1;1;0} , {150;50;50;0} , {150;0;10;0} ) - SUM(M6:M8)

= ( 1*150*150 + 1*50*0 + 1*50*10 + 0*0*0 ) - 15000

= 8000

The logic is to calculate the cumulative total cost of sales starting from the beginning by SUMPRODUCT(--(-SUM($L$6:L9)>$I$6:I9),-SUM($L$6:L9)-$I$6:I9,$K$6:K9) and subtract the previous cost of sales up to the last transaction with -SUM($M$6:M8). So, the remaining balance would be the non-cumulative cost of sales for that particular transaction. Hope this is clearer.

[grossal]

We are getting closer! @AustinLeung 

If you sum up every cost in the excel per stock and in my version - both are equal. I am currently trying to figure out the last details to make them exactly equal.

e.g.

Apple [Excel] = 800

Apple [Me]    = 800

Banana [Excel] = 15000+8000 = 23000

Banana [Me]     = 22500 + 500 = 23000

...

[AustinLeung]

Great! So glad to hear that. Would you mind sharing the file so that I could have a look on what you are doing? Thanks a lot!

[AustinLeung]

@grossal, I guess we could use Run Total as the last step?

[reply_mueller · Accepted solution]

Hey @AustinLeung , hey @grossal ,

I really liked your problem, since it is quite tricky and intriguing. At a first glance, I thought I could solve this using only standard tools, like @grossal  tried.

I actually succeeded in creating a solution for your example data, but shortly before posting I came to realize that this won't work for more complex scenarios.

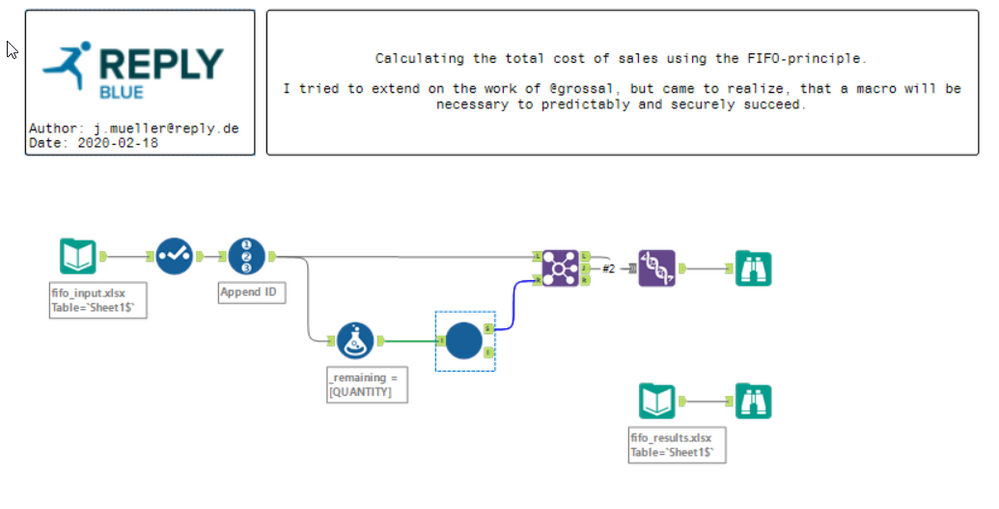
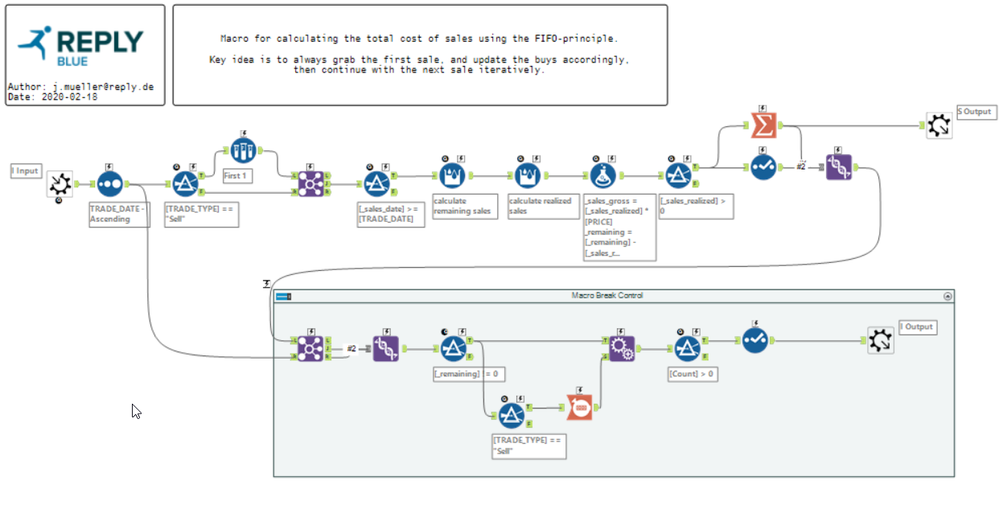
Therefore I introduced (nearly) the same code in an iterative macro which, for each iteration takes one sale and collects its respective buys.

After calculating the amount of sold units, the remaining stock of the buys is updated and the sale is removed from the list.

The tool box in the lower part of the macro serves mostly to control the macros flow.

I hope this could solve your problem.

Best, 

Johannes

(Blue Reply)

[AustinLeung]

Hi Muller,

I have been trying to use @grossal approach but also find that the logic does not work for more complex scenarios.

I am still trying to understand your work but I have tested a few samples and that works!

I will try to apply the model to my actual data and see if all is fine. Thank you very much for your help!

[DavidP · Accepted solution]

As @reply_mueller said, this was a really interesting problem, possibly even one for @JoeS to have a look at for a weekly challenge! Ever since you first posted it, I've been mulling it over, scribbling notes on random pieces of paper, mumbling away to myself, etc.

As Johannes also realized, I knew that an iterative macro would solve it, but I was obsessed with finding another way.

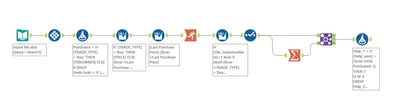
I finally settled on the following idea. Convert all the buy events and sell event to rows with a quantity of 1. Then the FIFO principle becomes easier to implement.

My solution attached below