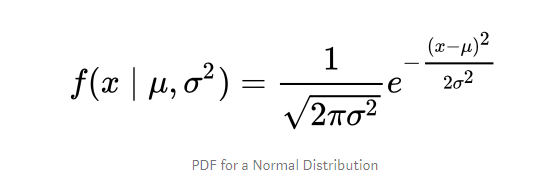Create Table for Bell Curve

[Shelton_Thompson]

I am trying to use alteryx to create a table for a bell curve visual in PowerBI because PowerBI does not have a dynamic table capability (yet). 

My initial data is the following (just a sample)

Request ID	Total Time Taken	FY	Created Date
1	5	18/19	07/18/2019
2	10	18/19	07/01/2019
3	20	17/18	08/01/2017
4	30	17/18	01/01/2018

Using the summarize tool, I have performed the following actions on the data:

• Group by FY
• Min of Created Date
• Max of Created Date
• AvgNo0 of Total Time Taken
• StdDevNo0 of Total Time Taken
• Min  of Total Time Taken
• Max  of Total Time Taken

I then use a formula tool to create the x-3a and x+3a values (i.e. the min and max's of the array for the bell curve) 'x' being the mean and 'a' being the standard deviation.

I then use a generate rows tool to generate the array ranges for each fiscal year. 

This results in the following which is what I want. 

FY	Min_Created Date-Date Only	Max_Created Date-Date Only	Mean	Standard Dev	Min_Total Time (Business Days)	Max_Total Time (Business Days)	X-3A	X+3a	Value
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-18
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-17
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-16
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-15
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-14
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-13
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-12
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-11
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-10
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-9
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-8
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-7
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-6
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-5
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-4
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-3
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-2
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	-1
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	0
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	1
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	2
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	3
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	4
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	5
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	6
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	7
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	8
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	9
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	10
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	11
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	12
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	13
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	14
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	15
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	16
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	17
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	18
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	19
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	20
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	21
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	22
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	23
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	24
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	25
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	26
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	27
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	28
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	29
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	30
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	31
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	32
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	33
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	34
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	35
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	36
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	37
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	38
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	39
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	40
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	41
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	42
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	43
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	44
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	45
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	46
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	47
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	48
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	49
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	50
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	51
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	52
16/17	10/3/2016	5/31/2017	17	12	0.01	113.1	-18	53	53
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-10
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-9
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-8
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-7
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-6
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-5
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-4
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-3
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-2
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	-1
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	0
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	1
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	2
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	3
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	4
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	5
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	6
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	7
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	8
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	9
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	10
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	11
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	12
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	13
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	14
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	15
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	16
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	17
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	18
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	19
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	20
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	21
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	22
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	23
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	24
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	25
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	26
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	27
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	28
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	29
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	30
17/18	6/1/2017	5/31/2018	10	7	0.19	64.47	-10	31	31
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-10
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-9
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-8
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-7
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-6
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-5
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-4
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-3
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-2
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	-1
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	0
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	1
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	2
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	3
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	4
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	5
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	6
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	7
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	8
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	9
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	10
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	11
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	12
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	13
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	14
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	15
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	16
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	17
18/19	6/1/2018	5/31/2019	4	5	0.01	49.59	-10	18	18
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	-6
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	-5
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	-4
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	-3
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	-2
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	-1
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	0
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	1
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	2
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	3
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	4
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	5
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	6
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	7
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	8
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	9
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	10
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	11
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	12
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	13
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	14
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	15
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	16
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	17
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	18
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	19
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	20
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	21
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	22
19/20	6/2/2019	7/10/2019	8	5	0.02	24.56	-6	23	23

Next, I need to do the following and this is where I am stuck trying to figure out how to do this. 

1. Calculate the Norm Distribution for each array value. In excel this is =NORM.DIST([ARRAYVALUE],[MEAN],[STND DEV],FALSE)
2. Calculate the ranges within the bell curve array for the Total Time Taken 
3. Count how many requests fall into each region and then calculate a percentage

Ultimately in PowerBI, I want to end up with something like the following but also include labels of the Total Time Taken and the counts and percentages but in order to do this, I need to feed PowerBI the table or tables.

Open to any suggestions on how to do this or if potentially there is a better way to do this...

[danilang]

Hi @Shelton_Thompson 

I can get you the next step of the way.  Using this formula taken from here,  the attached  workflow calculates the y values for your bell curves using this formula

which translates to this in Alteryx

1/SQRT(2*pi()*pow([Standard Dev],2))*exp(-pow(([Value]-[Mean]),2)/(2*pow([Standard Dev],2)))

Dan

[Shelton_Thompson]

Thank you! That works perfectly! now just have to figure out how to plot the points to show the average time taken at each point and get the percentages to define the areas.

Reading your link my 'theory' is I could calculate the z-score for each record, then use a standard normal distribution table to determine the percentage and plotting values. Not sure yet how I will make that work, but time to play! If anyone has any ideas in the meantime, I am open to them!

[Shelton_Thompson · Accepted solution]

Alright I got it! I took it a step further and also created a Macro so no one else has to try to figure this out with a built-in Standard Normalization Table. 

https://gallery.alteryx.com/#!app/Bell%2BCurve/5d3739e0826fd3108052ad22