Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Challenge #270: Pony Permutations
Challenge #270: Pony Permutations
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A solution to last week's challenge can be found here. 
This week's challenge was submitted by @mst3k - Thank you for your submission!
Later this week, the Belmont Stakes will be held in New York. If you are unfamiliar, this is a famous horse race which serves as the third race in the Triple Crown (the Kentucky Derby and Preakness are the other two legs). While there will not be a triple crown winner this year (since different horses won the previous two legs), we can still have some fun analyzing some race possibilities!
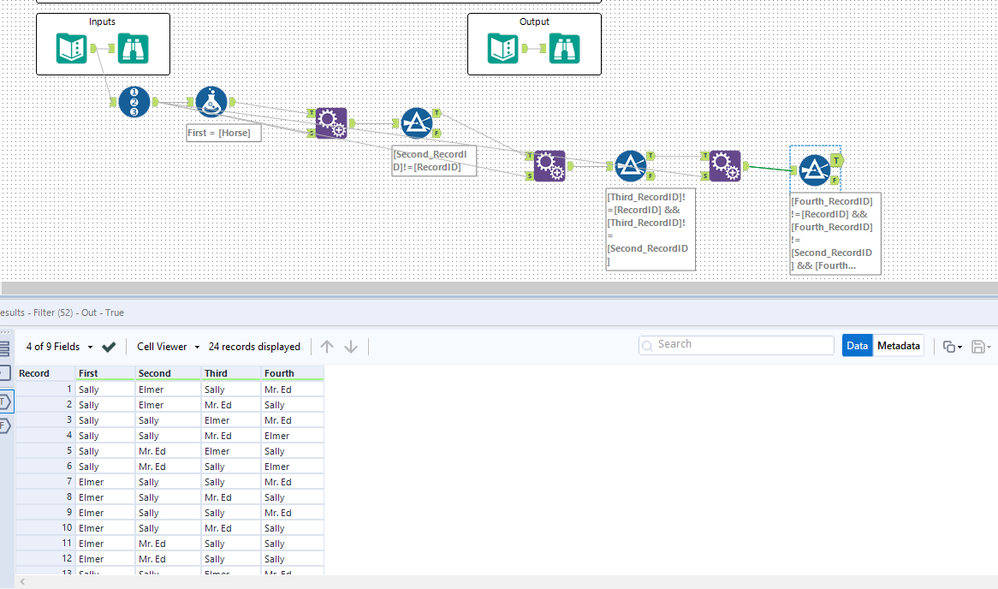
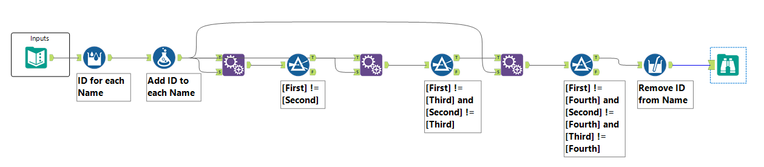
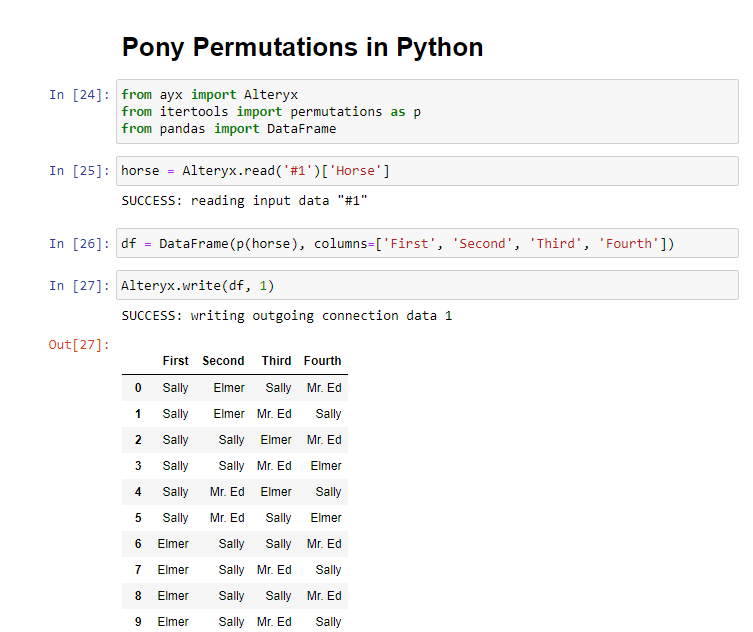
A race is being held between 4 horses. Create an output of every possible combination of race finishes. No horse should be able to finish in more than 1 place, but be warned there are two *different* mustangs named Sally in this race!
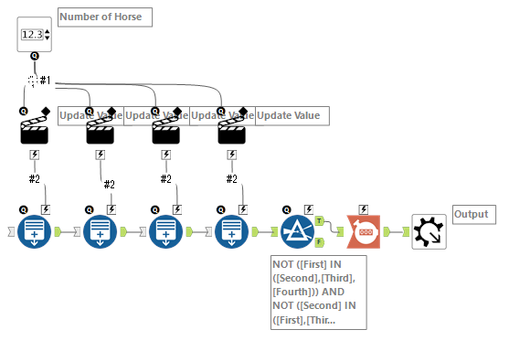
Extra Credit: If there are 5 horses instead of 4, how many possible outcomes are there? Can that number be generalized if there are n number of horses?
- Labels:
-
Basic
-
Core
-
Data Analysis
-
Join
-
Preparation
-
Transform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@estherb47 Does this bring back nightmares of Born to Solve Nashville?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
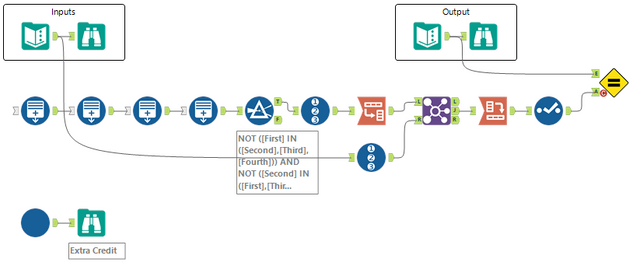
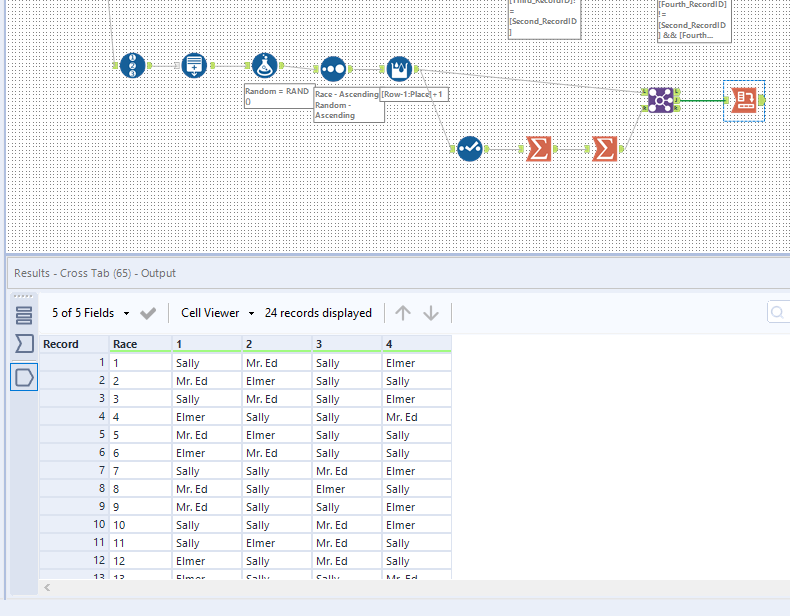
And to solve the advanced part/make it more dynamic without macros, we can simulate enough horse races to get all the possible outcomes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
fun fact: race horse names cannot be reused until 5 years after the horse has stopped racing or breeding
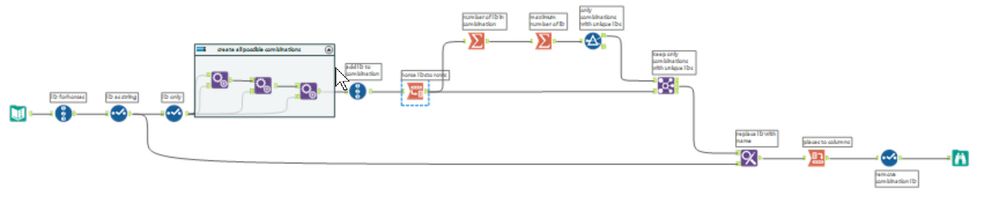
I believe the number of solutions for this problem is just a simple factorial? So it should generalize to any number of starters.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
-
Advanced
301 -
Apps
26 -
Basic
158 -
Calgary
1 -
Core
157 -
Data Analysis
185 -
Data Cleansing
5 -
Data Investigation
7 -
Data Parsing
14 -
Data Preparation
238 -
Developer
36 -
Difficult
86 -
Expert
16 -
Foundation
13 -
Interface
39 -
Intermediate
268 -
Join
211 -
Macros
62 -
Parse
141 -
Predictive
20 -
Predictive Analysis
14 -
Preparation
272 -
Reporting
55 -
Reporting and Visualization
16 -
Spatial
60 -
Spatial Analysis
52 -
Time Series
1 -
Transform
227
- « Previous
- Next »