Alteryx Designer Desktop Discussions
Find answers, ask questions, and share expertise about Alteryx Designer Desktop and Intelligence Suite.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- Designer Desktop
- :
- Re: Understanding the Linear Regression Output
Understanding the Linear Regression Output
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I am trying to check the possibility of creating a prediction model on the basis of variables i have, in a data set. For this, i am checking various predictor variables relationships with the target variable. I am using Linear Regression technique to check the same.
Below is a result of one such run:
From this, i could see that Pr and Significance(*) are showing that predictor variables have strong relationships with target variable. But the R-squared value shows a not very strong model. Is this a normal finding to have this differences among various parameters?
Solved! Go to Solution.
- Labels:
-
Predictive Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi @GauravRawal
You should meet with a statistician to go over your model. I've run into this when there is a strong relationship between the independent variables and the dependent variables, but there is a lot of variability in the data.
Here is a good place to start for understanding this situation:
Important points from the article:
The coefficients estimate the trends while R-squared represents the scatter around the regression line.
The interpretations of the significant variables are the same for both high and low R-squared models.
Low R-squared values are problematic when you need precise predictions.
So, what’s to be done if you have significant predictors but a low R-squared value? I can hear some of you saying, "add more variables to the model!"
In some cases, it’s possible that additional predictors can increase the true explanatory power of the model. However, in other cases, the data contain an inherently higher amount of unexplainable variability. For example, many psychology studies have R-squared values less that 50% because people are fairly unpredictable.
I'd be interested to see plots of the independent variables versus the dependent variables.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Philip for the detailed explanation.
I went through the link you provided and it made complete sense to me. As suggested by you, i will try to dig down more on what variables i am analyzing for prediction.
The point i want to clarify is: If there is a situation like this, the way to move forward is to analyze the predictor variable and check the variations by adding/removing different variables, from the model. If we still don't find a correct model, do we say that this problem is not predictive at all or we try for some other possible predictive modelling approach, on the same variables? Or we redefine the whole predictive problem itself and then work to create a model for the new problem?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's more of a statistical question that statisticians can answer better. Here are things from my experience:
1. When I've done regression-based predictive modeling, I've used half the data to develop the model, then the other half as a test set to see how the model performs predicting outcomes. The method for model development is to use a stepwise methodology. My statistics professor in university suggested to us to perform both forward and backward stepwise model selection and see if we arrive at the same model.
Forward selection: You begin with no candidate variables in the model. Select the variable that has the highest R-Squared. At each step, select the candidate variable that increases R-Squared the most. Stop adding variables when none of the remaining variables are significant. Note that once a variable enters the model, it cannot be deleted.
Backward selection: At each step, the variable that is the least significant is removed. This process continues until no nonsignificant variables remain. The user sets the significance level at which variables can be removed from the model.
2. With significant predictors but low Rsqr, I would tend to explain it as there is a relationship, but it has high variability. Any predictions made from this model should not be considered precise.
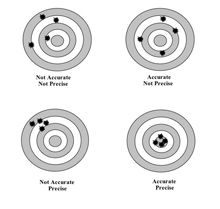
(See this: https://www.ncsu.edu/labwrite/Experimental%20Design/accuracyprecision.htm
Precision refers to the closeness of two or more measurements to each other. Using the example above, if you weigh a given substance five times, and get 3.2 kg each time, then your measurement is very precise. Precision is independent of accuracy. You can be very precise but inaccurate, as described above.
)
3. Having said that, I've seen public health and epidemiology studies present models with and Rsqr of 20% and seem very happy with it. This is because there is just so much variability in human and environmental interactions related to a disease outcome. However, this was more for understanding relationships than trying to develop a predictive model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have to second everything that Philip has already said. Philip mentioned that R squares can vary based on the data set. When I do marketing analysis, a good R squared is around 15%, but an average on is 5%. Some of the things we look at just have a wide degree of variability.
You may be looking at a situation where a simple linear model is not what is called for. You may need an interacted model, or a non-linear model. Alteryx is great for running simple linear models, but anything more complicated needs to be run in a stats program.
As Philip suggested, you may need to have a conversation with a statistician, or an ecnometrician. There are a variety of more sophisticated options that are available.
From personal experience, the more complicated models are rarely needed. I've had models like your's that had low R squared. I switched them over to R, and ran all sorts of complicated stuff. Non-linear, interacted, and Simultaneous. In the end I found that the simple linear was the best model about 75% of the time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi @GauravRawal @charity_wilson,
Thanks for your continued support. To help user understand the models and variable importance better, we recently published a new model explanation macros: LIME here.
It supports both Regression & Classification predictive tools including Linear regression, SVM, Decision Tree, Gradient Boosted, etc. Give a try and hope it could give you a hand.
-
Academy
6 -
ADAPT
2 -
Adobe
204 -
Advent of Code
3 -
Alias Manager
78 -
Alteryx Copilot
26 -
Alteryx Designer
7 -
Alteryx Editions
95 -
Alteryx Practice
20 -
Amazon S3
149 -
AMP Engine
252 -
Announcement
1 -
API
1,208 -
App Builder
116 -
Apps
1,360 -
Assets | Wealth Management
1 -
Basic Creator
15 -
Batch Macro
1,559 -
Behavior Analysis
246 -
Best Practices
2,695 -
Bug
719 -
Bugs & Issues
1 -
Calgary
67 -
CASS
53 -
Chained App
268 -
Common Use Cases
3,825 -
Community
26 -
Computer Vision
86 -
Connectors
1,426 -
Conversation Starter
3 -
COVID-19
1 -
Custom Formula Function
1 -
Custom Tools
1,938 -
Data
1 -
Data Challenge
10 -
Data Investigation
3,487 -
Data Science
3 -
Database Connection
2,220 -
Datasets
5,222 -
Date Time
3,227 -
Demographic Analysis
186 -
Designer Cloud
742 -
Developer
4,372 -
Developer Tools
3,530 -
Documentation
527 -
Download
1,037 -
Dynamic Processing
2,939 -
Email
928 -
Engine
145 -
Enterprise (Edition)
1 -
Error Message
2,258 -
Events
198 -
Expression
1,868 -
Financial Services
1 -
Full Creator
2 -
Fun
2 -
Fuzzy Match
712 -
Gallery
666 -
GenAI Tools
3 -
General
2 -
Google Analytics
155 -
Help
4,708 -
In Database
966 -
Input
4,293 -
Installation
361 -
Interface Tools
1,901 -
Iterative Macro
1,094 -
Join
1,958 -
Licensing
252 -
Location Optimizer
60 -
Machine Learning
260 -
Macros
2,864 -
Marketo
12 -
Marketplace
23 -
MongoDB
82 -
Off-Topic
5 -
Optimization
751 -
Output
5,255 -
Parse
2,328 -
Power BI
228 -
Predictive Analysis
937 -
Preparation
5,169 -
Prescriptive Analytics
206 -
Professional (Edition)
4 -
Publish
257 -
Python
855 -
Qlik
39 -
Question
1 -
Questions
2 -
R Tool
476 -
Regex
2,339 -
Reporting
2,434 -
Resource
1 -
Run Command
575 -
Salesforce
277 -
Scheduler
411 -
Search Feedback
3 -
Server
630 -
Settings
935 -
Setup & Configuration
3 -
Sharepoint
627 -
Spatial Analysis
599 -
Starter (Edition)
1 -
Tableau
512 -
Tax & Audit
1 -
Text Mining
468 -
Thursday Thought
4 -
Time Series
431 -
Tips and Tricks
4,187 -
Topic of Interest
1,126 -
Transformation
3,730 -
Twitter
23 -
Udacity
84 -
Updates
1 -
Viewer
3 -
Workflow
9,980
- « Previous
- Next »