Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Challenge #420: The Sierpinski Triangle
Challenge #420: The Sierpinski Triangle
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Maveryx,
A solution to last week’s challenge can be found here.
This week, we are diving deep into the realms of Math and Spatial tools by tackling the creation of Sierpinski’s triangle fractal. This challenge, designed by Roland van Leeuwen @RWvanLeeuwen, is an Expert-level task. If you are preparing for certification and plan to attempt an exam during Inspire, it is an excellent opportunity to hone your skills. Thank you, Roland, for crafting this challenge!
What is a Sierpinski triangle?
A Sierpinski triangle is a fractal shape composed of smaller triangles, each a scaled-down replica of the whole. It is created by repeatedly dividing an equilateral triangle into smaller triangles and removing the middle triangle at each iteration. This process results in a geometric pattern that exhibits self-similarity at different scales, forming a visually striking and intricate triangle-based fractal.
(This definition is sourced from https://en.wikipedia.org/wiki/Sierpi%C5%84ski_triangle.)
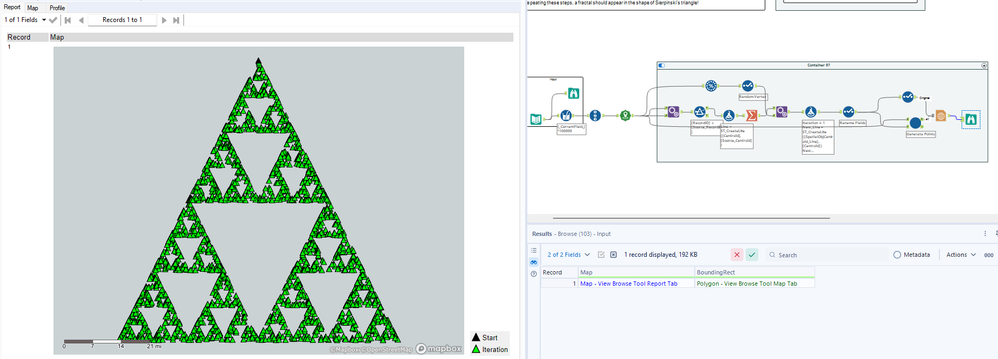
The provided input consists of the of latitude, longitude, and corners a, b, and c. (The corners are used to determine each point of the triangle.) Your output triangle will look like this:
For this challenge, we are providing additional guidance to simplify the tasks and help you build your Sierpinski’s triangle.
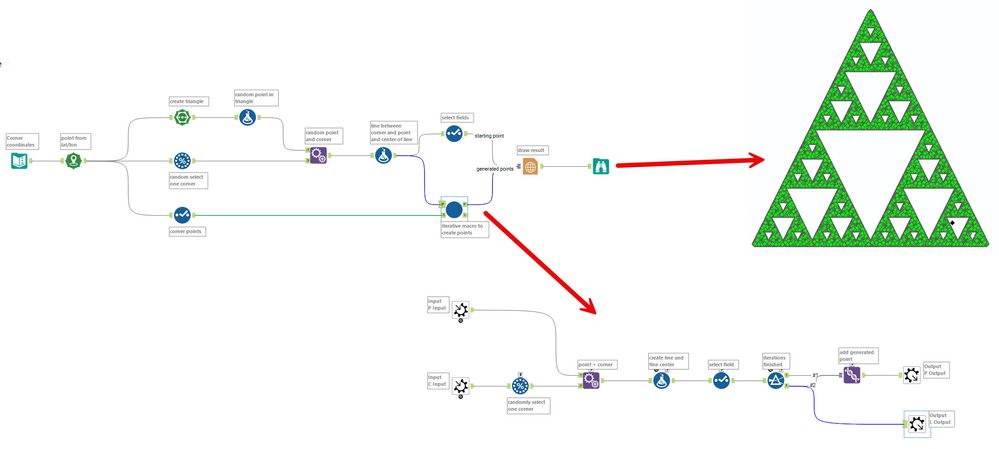
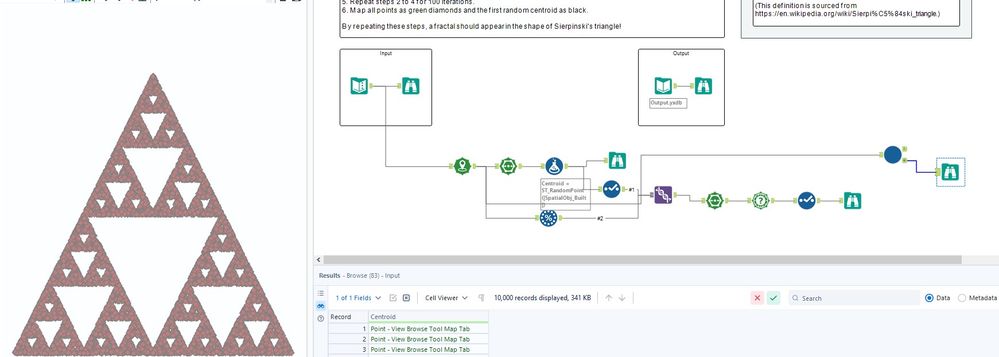
To construct a fractal triangle, follow these steps:
- Find the corners (points a, b, and c), and any random point within the triangle as a starting point.
- Select one of the corners of the triangle and form a line from the point to the corner.
- The center point of the line created is the one we will iterate with.
- Using the center point of the created line, pick another random corner, draw a line, and find its center.
- Repeat steps 2 to 4 for 100 iterations.
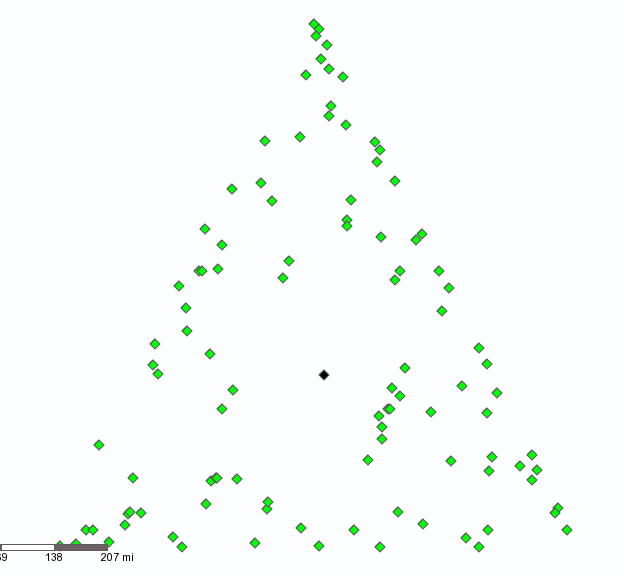
- Map all points as green diamonds and the first random centroid as black.
By repeating these steps, a fractal should appear in the shape of Sierpinski's triangle!
If you need a refresher on how to build an iterative macro or create spatial objects, review these lessons in Academy to gear up:
Good luck!
- Labels:
-
Difficult
-
Expert
-
Macros
-
Spatial Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This definitely seems like a @patrick_digan math problem

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
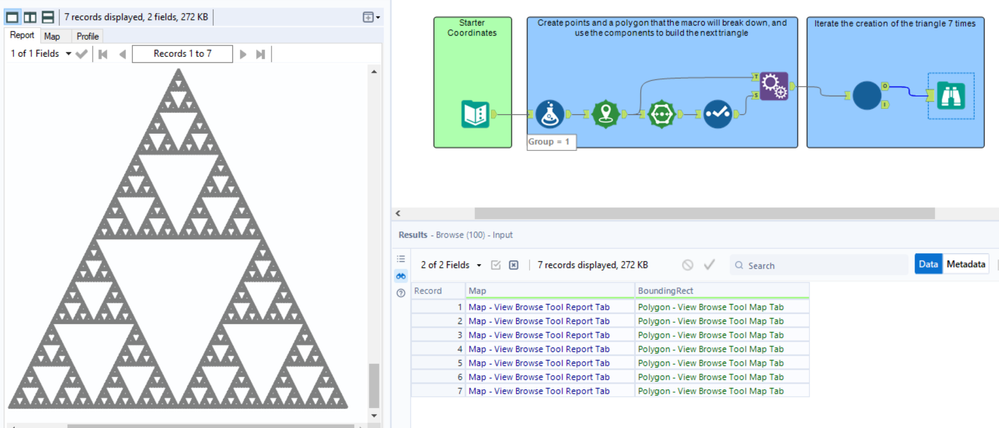
Oof, this was a doozy. More in spoiler
Also, I iterated it 2000 times for a more holistic picture.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That was fascinating. Having a hard time with why the algorithm works from any point but it sure does.
Needed a lot more than 100 iterations to get something filled out. Wonder if that meant 100, from each existing point each time.
I just kicked it up to 10k and the pattern emerges.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I like math, I like this challenge.
When it comes to a challenge associated with Iteration Macro, it's very quiet here. It implies that Iterative operation in Alteryx would be one of the hurdle for the most users.
To create a random point, ST_RandomPoint([obj]) is very handy.
Some observation:
(1) We need at least 1,000 iterations to get a vivid view, we are instructed to go with 100 iterations though. If your computer allows, go with 100k.
100

1k

10k

(2) Point created during the first 2 iterations sometimes fall outside the triangle(sometime not). I omitted the record from first 2 iterations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Math is really magical.
100 Iterations
30K iterations

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
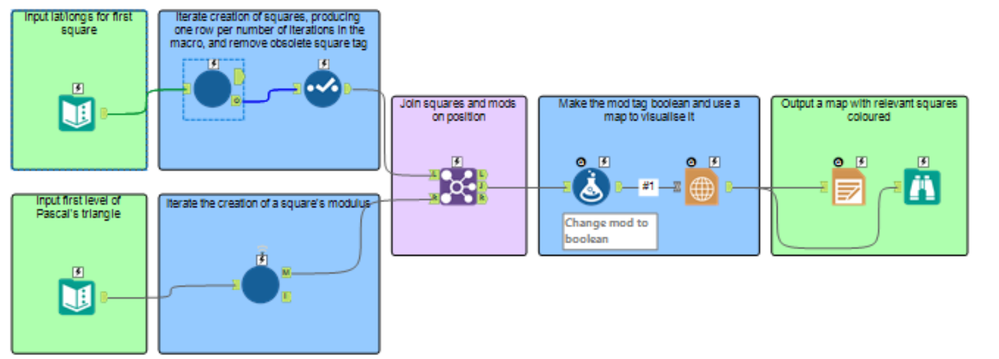
Great challenge! I posted a similar challenge before on Databasyx.com so I've gone a bit rogue and have a couple of other ways to create the Sierpinski triangle in Alteryx!
One way is similar to this challenge with using midpoints but cutting out shapes instead using spatial process. The other is to colour in every even number in a Pascal's Triangle!
Edit: Pictures in below post. Failed to upload and couldn't edit them in!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Apologies for double post but pictures failed to upload in my previous post and can't edit them in still!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
-
Advanced
302 -
Apps
27 -
Basic
158 -
Calgary
1 -
Core
157 -
Data Analysis
185 -
Data Cleansing
5 -
Data Investigation
7 -
Data Parsing
14 -
Data Preparation
238 -
Developer
36 -
Difficult
87 -
Expert
16 -
Foundation
13 -
Interface
39 -
Intermediate
268 -
Join
211 -
Macros
62 -
Parse
141 -
Predictive
20 -
Predictive Analysis
14 -
Preparation
272 -
Reporting
55 -
Reporting and Visualization
16 -
Spatial
60 -
Spatial Analysis
52 -
Time Series
1 -
Transform
227
- « Previous
- Next »