Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Challenge #140: Prove the Birthday Paradox!
Challenge #140: Prove the Birthday Paradox!
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
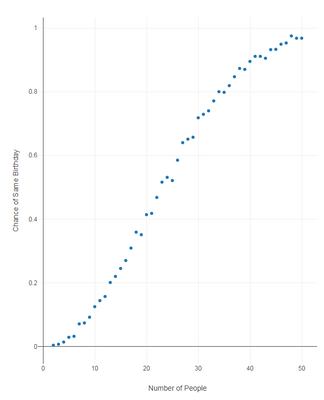
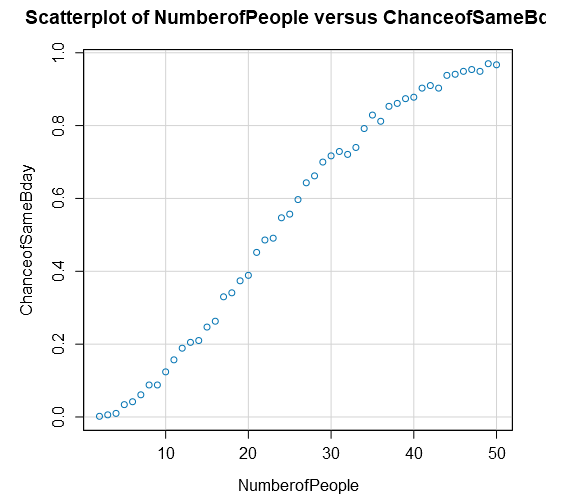
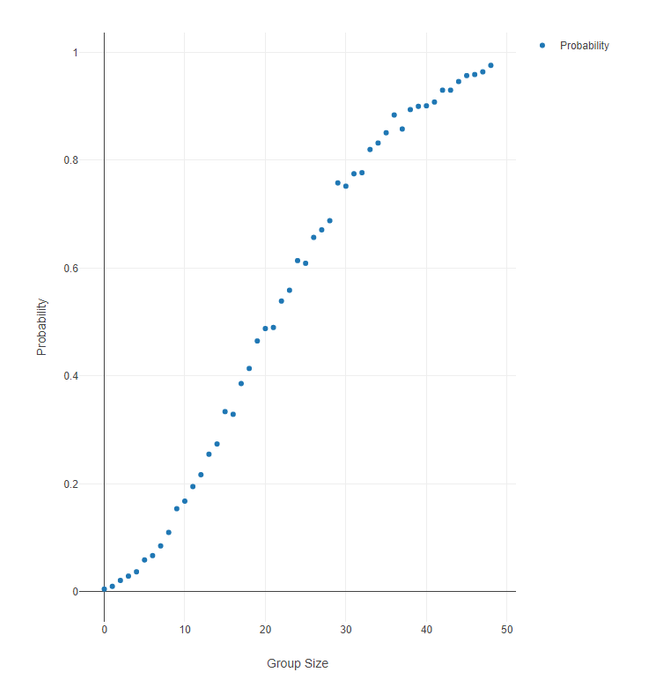
This week we will run an anecdotal workflow to prove the Birthday Paradox! The Birthday paradox simply refers to the phenomenon that if you assembled 23 people into one room, the chances of two people having the same birthday are 50-50. We could 'math' this out, but why not just assembles 100s of thousands of people in the seconds to prove it?
In this challenge, your goal is to build a table that increment group sizes from 2 people all the way to 50 people. In each of those group sizes, run 1000 random trials and see what percent of groups had at least one set of people match. Why 1000? Theoretically, the more trials you run, the more likely you are to get a refined percent (e.g. flipping a coin four times may not a perfect 50-50 chance where it would be much closer after 1000 flips).
Due to the nature of this challenge, you will need to generate your own data! I have provided a sample output of mine, but since we are randomly assigning birthdays, you may find small differences in our answers. At what group size did it exceed 75% chance? 90% chance?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
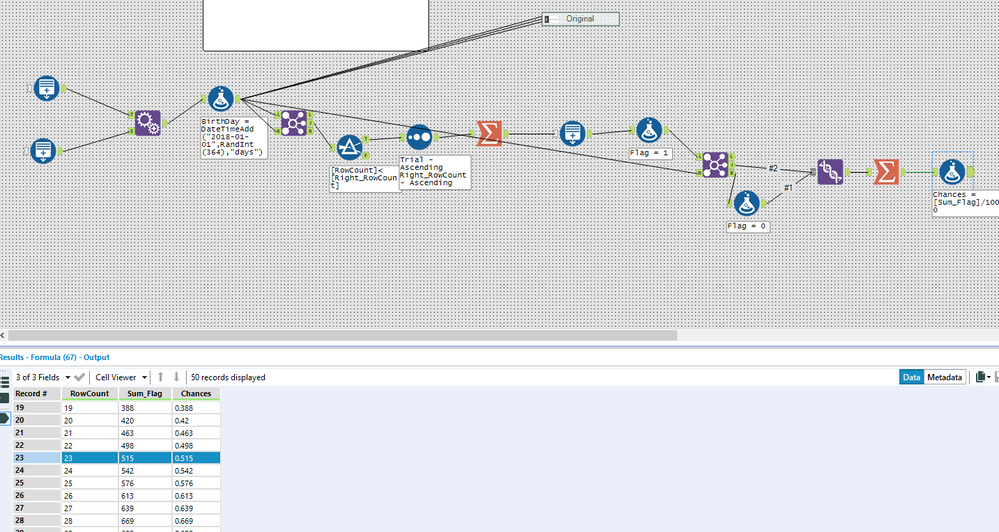
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
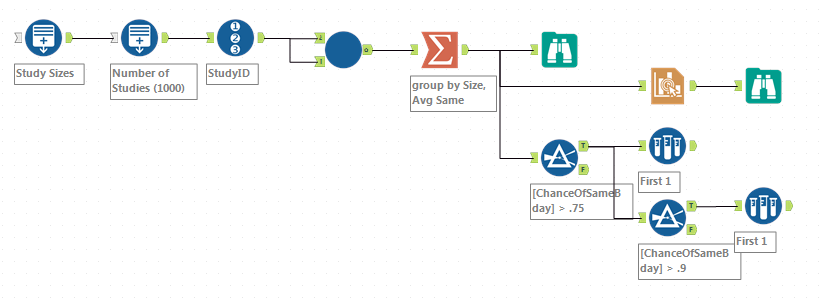
Started off with an iterative macro but just ended up with a brute force method.
Check out my collaboration with fellow ACE Joshua Burkhow at AlterTricks.com
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
 incorporating the macro, aggregating the data and creating the viz
incorporating the macro, aggregating the data and creating the viz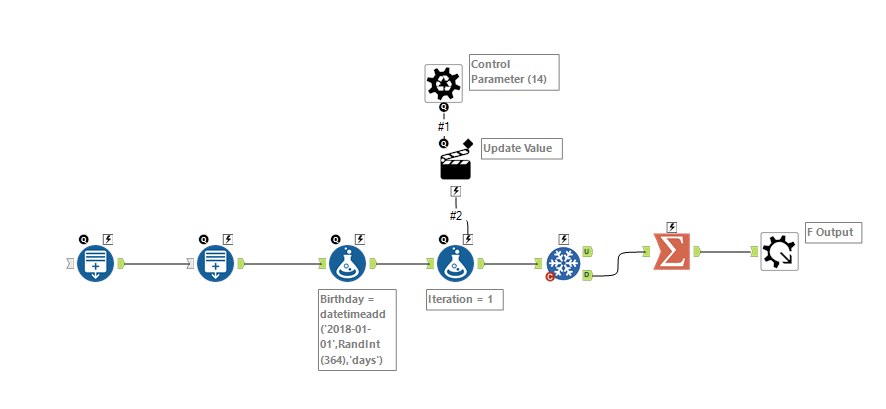 batch macro, one per trial
batch macro, one per trial- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
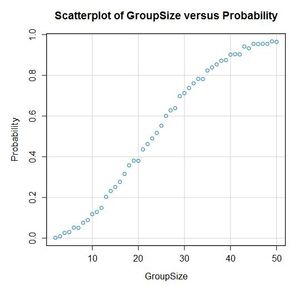
Studied this one as part of my degree :D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cheers! That was a lot of fun!
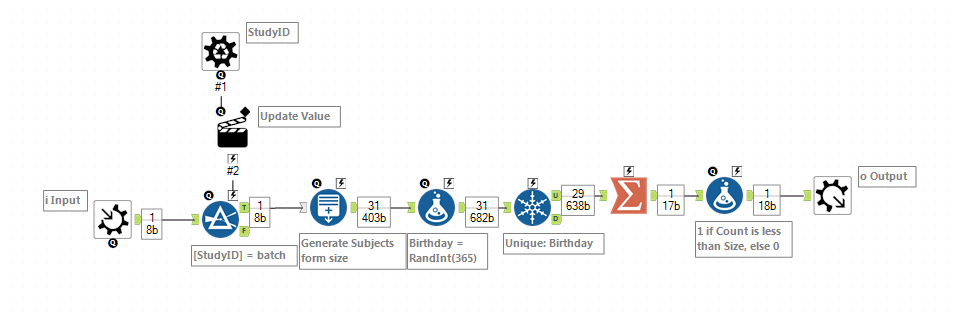
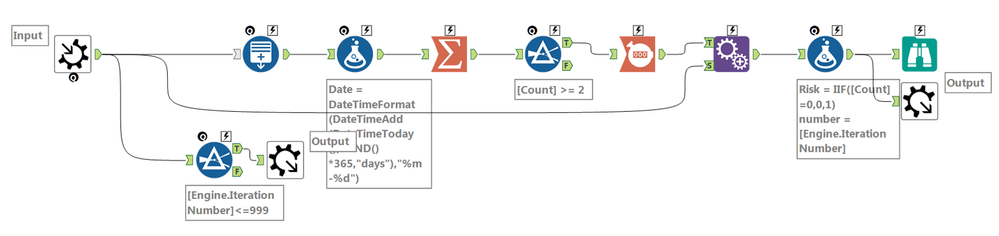 Iterative Macro
Iterative Macro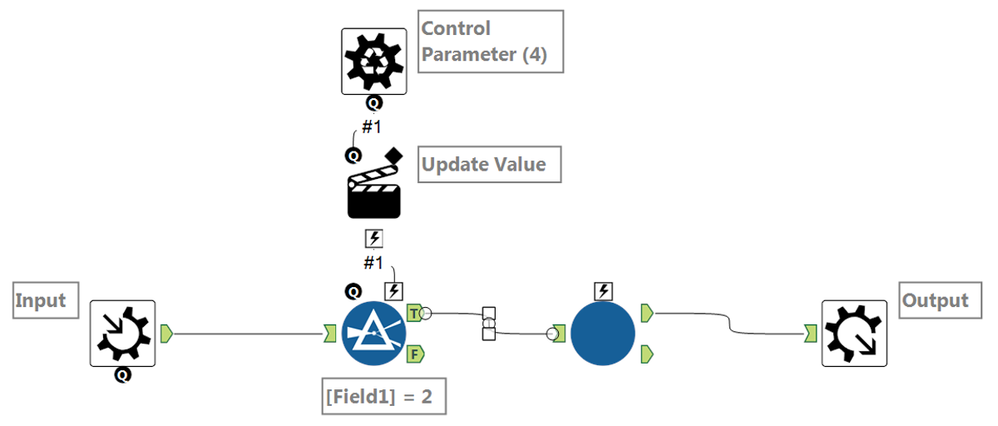 Batch Macro
Batch Macro- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
-
Advanced
302 -
Apps
27 -
Basic
158 -
Calgary
1 -
Core
157 -
Data Analysis
185 -
Data Cleansing
5 -
Data Investigation
7 -
Data Parsing
14 -
Data Preparation
238 -
Developer
36 -
Difficult
87 -
Expert
16 -
Foundation
13 -
Interface
39 -
Intermediate
268 -
Join
211 -
Macros
62 -
Parse
141 -
Predictive
20 -
Predictive Analysis
14 -
Preparation
272 -
Reporting
55 -
Reporting and Visualization
16 -
Spatial
60 -
Spatial Analysis
52 -
Time Series
1 -
Transform
227
- « Previous
- Next »