Difference in R^2 between linear regression and decision tree model

[chasejancek]

I am trying to create a regression model to predict sales. When I run my data with the Linear Regression tool I get an R-squared value of .046. When I run it through the decision tree I get .71, which is much better. 

I am using the same variables in both models and not changing any other configurations. Could anyone tell me why there is such a large discrepancy between R^2 values?

[CharlieS]

Hi @chasejancek 

There's a lot more to predictive modeling than a getting a high R^2 value. Selecting the appropriate model type is an important first step.If you're building a model to predict sales, the continuous nature of that dependent variable should guide the types of models tested. A linear regression is the more appropriate choice for this scenario, whereas a Decision Tree model is more appropriate for classification scenarios. 

[danilang · Accepted solution]

Hi @chasejancek 

It's difficult to say without actually seeing your data, but it probably has to do it's "shape".  By "shape", what I mean is, what is type of correlation is there between the dependent and independent variables.   If the data has a linear correlation built into it, then a linear regression will model it with a large R^2 value.  For example, where I'm from, amount of snow left on the ground in March has as strong linear correlation to the amount of snow that has fallen since the previous November.  The relationship isn't perfectly linear because there is some temperature induced variation.   If the underlying data has a different distribution, i.e. it's normally distributed, linear regression will still produce a result, but the R^2 error will be much smaller.

The decision tree model is more complex and is able to find sub groups within the data that share common correlation characteristics.  It's able to take a normal distribution and split it into groups that minimize the R^2  

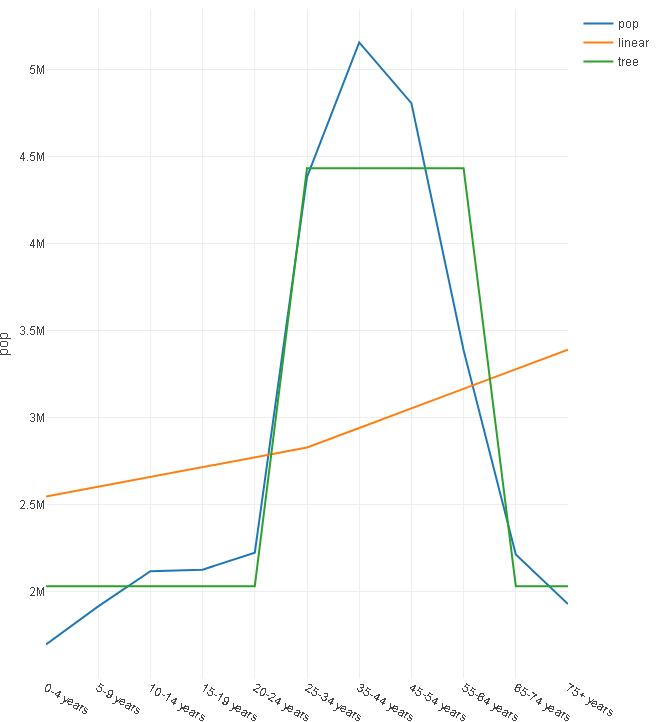
The following data models a hypothetical population distribution based on age(Blue line).  The mustard colored line is the output of the Linear regression tool.  The green one was created using a Decision Tree tool.

Because the underlying data is not linear, the decision tree was able to model it with a higher R^2 (=.8) than the linear regression (R^2 = 0.01).

You need to have some understanding of your data in order to pick the correct model to apply

This is part of what makes statistics so much fun!

Dan