General Discussions
Discuss any topics that are not product-specific here.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- General
- :
- Re: Advent of Code 2020 - BaseA Style (Day 13)
Advent of Code 2020 - BaseA Style (Day 13)
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Discussion thread for day 13 of the Advent of Code : https://adventofcode.com/2020/day/13
- Labels:
-
Advent of Code
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
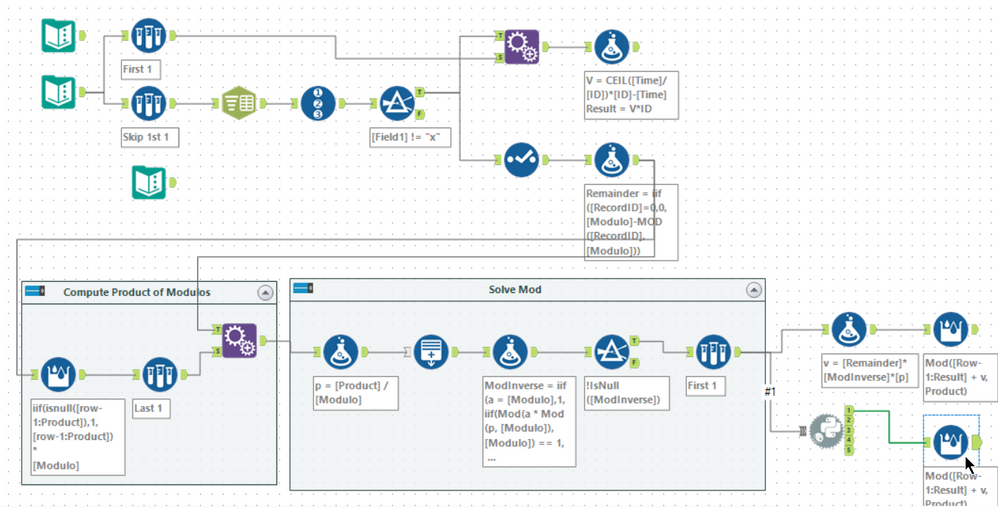
Here's my Part A.

Added in the tools at the end to get to single cell answer.
Part B I don't think is an iterative macro, I think it's a case of getting a calculator out.
Check out my collaboration with fellow ACE Joshua Burkhow at AlterTricks.com
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's my solve - BaseA for 95% but needed some true integer maths for last part
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
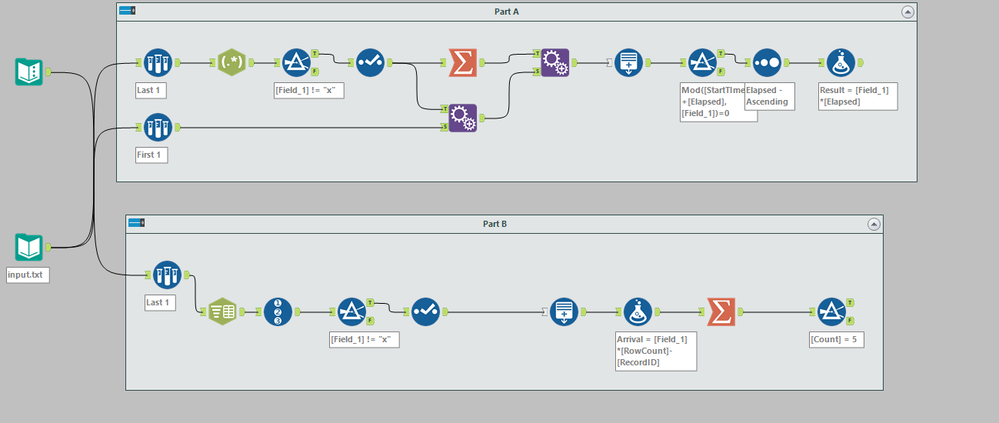
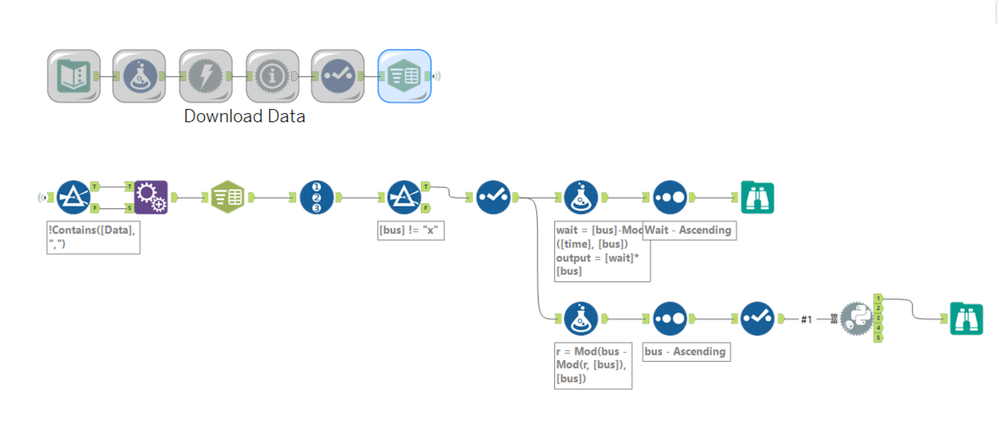
Here's my part A and part B, though only for the sample problem. As @jdunkerley79 mentioned, Int64 operations are required for the full solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I caved and am using python for part 2 because I don't have the brain power to create a modinv() function from scratch in Alteryx
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
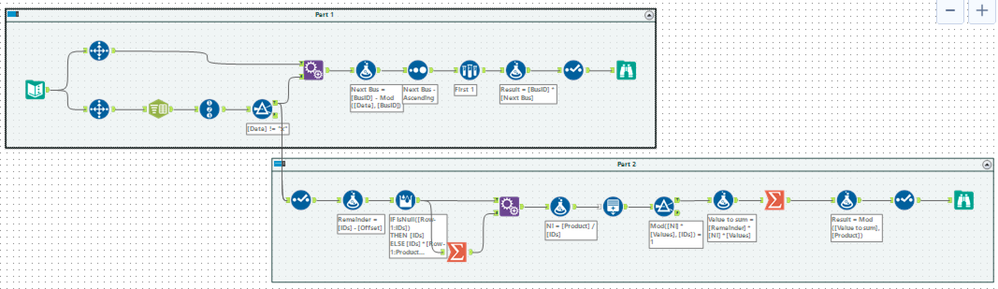
Part 2
replicated it in Alteryx and could get the examples working in Alteryx but couldn't get the final answer exactly as required.
Imagine it's something to do with the modulo function on very large numbers losing a bit of accuracy, so got the exact answer using https://www.dcode.fr/chinese-remainder (my answer is out by 198).
Then added a generate rows to go 300 numbers either side of the output generated by Alteryx and then use a modulo on the numbers to find the answer which matches.
The part 2 in Alteryx looks like this:

Check out my collaboration with fellow ACE Joshua Burkhow at AlterTricks.com
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I need to use pen and paper I know I'm in trouble. What a brain melt! I did it baseA with an iterative, works with my input. Once the headache leaves, I'll try to read and see other people's solutions 😅
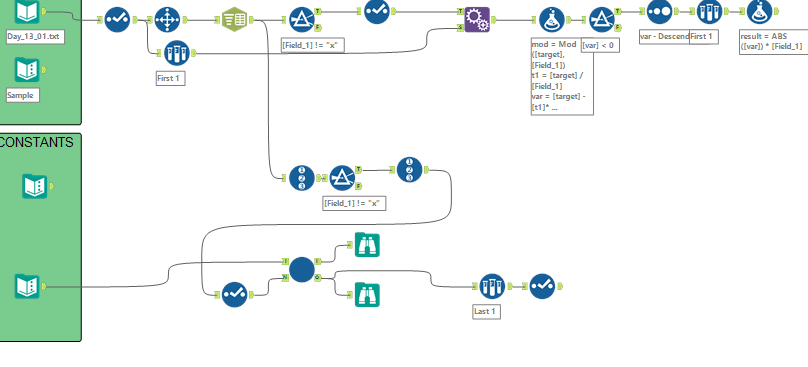
and the macro
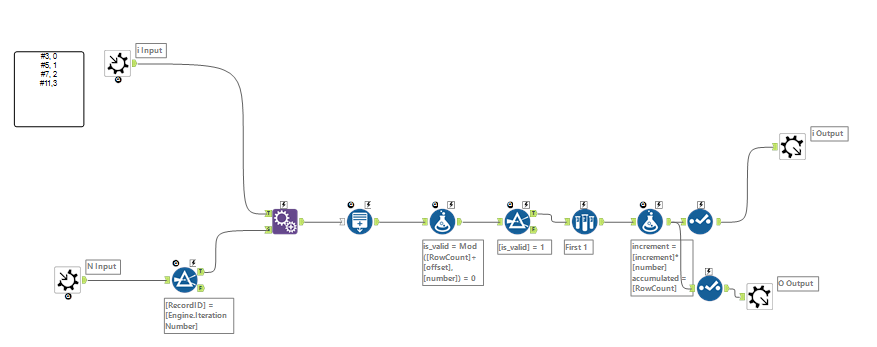
A summary of my thought process:
I started with
number 3, offset 0
number 5, offset 1
number 7, offset 2
number 11,offest 3
3&5 --> the first number that qualifies is 9 (mod(9,3) = 0 && mod(9+1,5)=0).
Then I need to find a number that qualifies for (3,5) and 7. I start with the first number that qualifies for the previous condition, go in increments of (3*5) --will all keep qualifying for mod(z,3) = 0, mod(z+1,5) = 0 -- until I find one that qualifies mod(z+2,7) = 0 (the first number that qualifies is 54)
For the next, I'll start at 54 and increase in increments of 105 (3*5*7) until I find one that qualifies mod(z+3,11) =0. (789).
And so on.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alteryx workflow with a python tool when needed
https://en.wikipedia.org/wiki/Modular_arithmetic
and grabbed a modinv() function from this stackoverflow page:
https://stackoverflow.com/questions/42049147/convert-list-to-pandas-dataframe-column
friends don't let friends reinvent the wheel 😅
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That part 2 really hurt my head. Discovered CRT after trying to find some relation between modulos and achieved to implement it in Alteryx but couldn't figure out the exact value. I guess it's due to accuracy problems, especially after @jdunkerley79 and @cgoodman replies. So used dcode tool to figure out the correct value. It's also on dcode that I studied and understood-ish the CRT.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Awesome solve @dsmdavid
My Abacus based solution is below. Needed to use it for 1 tool.
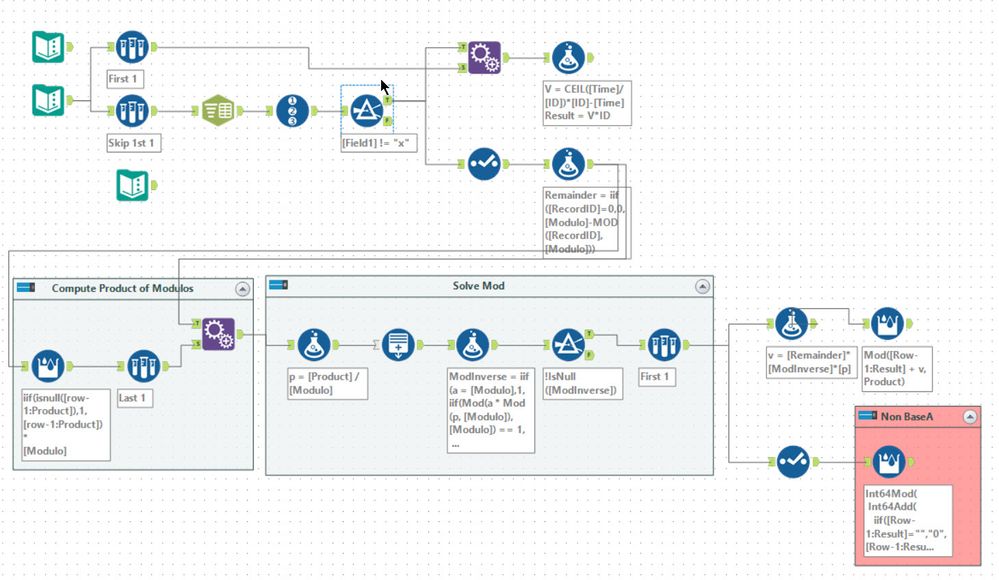
To correct the double maths issue. I converted the integers to strings and then used some new Abacus functions to compute as Int64
Int64Mod(
Int64Add(
iif([Row-1:Result]="","0",[Row-1:Result]),
Int64Mult([Remainder],[ModInverse],[p])
)
, [Product]
)-
.Next
1 -
2020.4
1 -
AAH
3 -
AAH Welcome
8 -
ABB
1 -
Academy
222 -
ADAPT
9 -
ADAPT Program
1 -
Admin
1 -
Administration
2 -
Advent of Code
135 -
AHH
1 -
ALTER.NEXT
1 -
Alteryx Editions
5 -
Alteryx Practice
442 -
Analytic Apps
6 -
Analytic Hub
2 -
Analytics Hub
4 -
Analyzer
1 -
Announcement
73 -
Announcements
25 -
API
3 -
App Builder
9 -
Apps
1 -
Authentication
3 -
Automation
1 -
Automotive
1 -
Banking
1 -
Basic Creator
5 -
Best Practices
3 -
BI + Analytics + Data Science
1 -
Bugs & Issues
1 -
Calgary
1 -
CASS
1 -
CData
1 -
Certification
270 -
Chained App
2 -
Clients
3 -
Common Use Cases
3 -
Community
817 -
Computer Vision
1 -
Configuration
1 -
Connect
1 -
Connecting
1 -
Content Management
4 -
Contest
49 -
Contests
1 -
Conversation Starter
159 -
COVID-19
15 -
Data
1 -
Data Analyse
2 -
Data Analyst
1 -
Data Challenge
188 -
Data Connection
1 -
Data Investigation
1 -
Data Science
102 -
Database Connection
1 -
Database Connections
3 -
Datasets
3 -
Date type
1 -
Designer
1 -
Designer Integration
4 -
Developer
5 -
Developer Tools
2 -
Directory
1 -
Documentation
1 -
Download
3 -
download tool
1 -
Dynamic Input
1 -
Dynamic Processing
1 -
dynamically create tables for input files
1 -
Email
2 -
employment
1 -
employment opportunites
1 -
Engine
1 -
Enhancement
1 -
Enhancements
2 -
Enterprise (Edition)
2 -
Error Messages
3 -
Event
1 -
Events
110 -
Excel
1 -
Feedback
2 -
File Browse
1 -
Financial Services
1 -
Full Creator
2 -
Fun
156 -
Gallery
2 -
General
23 -
General Suggestion
1 -
Guidelines
13 -
Help
72 -
hub
2 -
hub upgrade 2021.1
1 -
Input
1 -
Install
2 -
Installation
4 -
interactive charts
1 -
Introduction
25 -
jobs
2 -
Licensing
3 -
Machine Learning
2 -
Macros
3 -
Make app private
1 -
Marketplace
8 -
Maveryx Chatter
12 -
meeting
1 -
migrate data
1 -
Networking
1 -
New comer
1 -
New user
1 -
News
26 -
ODBC
1 -
Off-Topic
126 -
Online demo
1 -
Output
2 -
PowerBi
1 -
Predictive Analysis
1 -
Preparation
3 -
Product Feedback
1 -
Professional (Edition)
2 -
Project Euler
21 -
Public Gallery
1 -
Question
1 -
queued
1 -
R
1 -
Reporting
1 -
reporting tools
1 -
Requirements
1 -
Resource
117 -
resume
1 -
Run Workflows
10 -
Salesforce
1 -
Santalytics
9 -
Schedule Workflows
6 -
Search Feedback
76 -
Server
2 -
Settings
2 -
Setup & Configuration
5 -
Sharepoint
2 -
Starter (Edition)
2 -
survey
1 -
System Administration
4 -
Tax & Audit
1 -
text translator
1 -
Thursday Thought
57 -
Tips and Tricks
6 -
Tips on how to study for the core certification exam
1 -
Topic of Interest
167 -
Udacity
2 -
User Interface
2 -
User Management
5 -
Workflow
4 -
Workflows
1
- « Previous
- Next »