Tool Mastery
Explore a diverse compilation of articles that take an in-depth look at Designer tools.- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Tool Mastery
- :
- Tool Mastery | K-Centroids Diagnostics
Tool Mastery | K-Centroids Diagnostics
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
09-24-2018 06:32 AM - edited 08-03-2021 03:43 PM

This article is part of the Tool Mastery Series, a compilation of Knowledge Base contributions to introduce diverse working examples for Designer Tools. Here we’ll delve into uses of the K-CentroidsDiagnostics Tool on our way to mastering the Alteryx Designer:
Typically the first step of Cluster Analysis in Alteryx Designer, the K-Centroids Diagnostics Toolassists you to in determining an appropriate number of clusters to specify for a clustering solution in theK-Centroids Cluster Analysis Tool, given your data and specified clustering algorithm. Cluster analysis is an unsupervised learning algorithm, which means that there are no provided labels or targets for the algorithm to base its solution on. In some cases, you may know how many groups your data ought to be split into, but when this is not the case, you can use this tool to guide the number of target clusters your data most naturally divides into.
Configuration
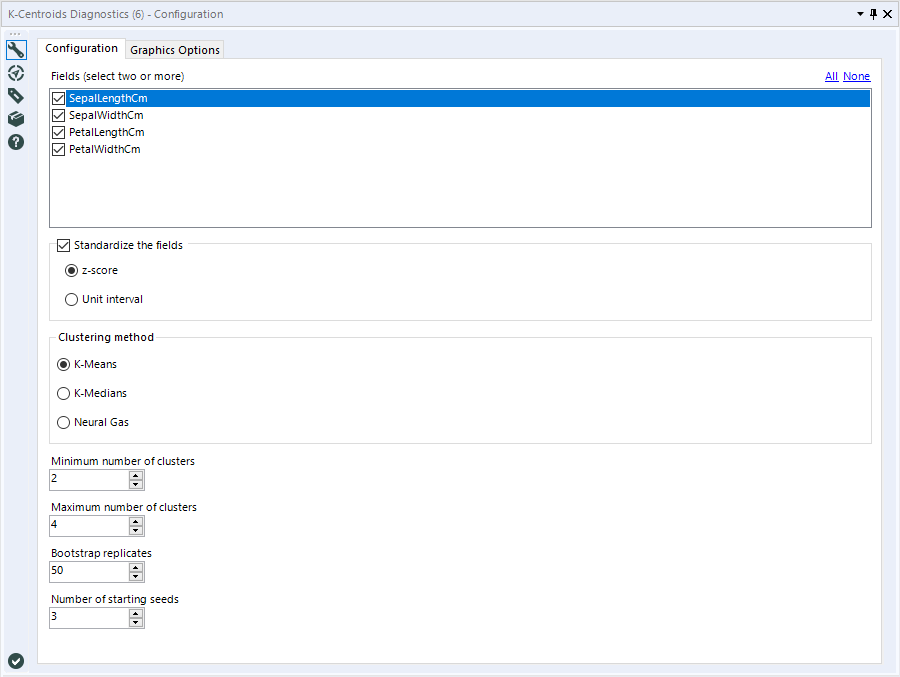
The first step of configuring this tool is to select the fields you are going to be performing your cluster analysis with. You should select each of the fields (and only the fields) you intend to create your clusters with. Because of how clustering algorithms work, only numeric fields will be populated as options.
As with the K-Centroids Cluster Analysis Tool, you have the option to standardize your fields. Clustering algorithms are very sensitive to the scale of the input data, so it is important to consider how standardizing might impact your results. If you intend to standardize your data in your clustering solution, you should select this option.
You have two options for standardization: Z-Score or Unit Interval. It is often considered best practice to standardize fields when performing cluster analysis. This is because of how distance (i.e., variable scale/magnitude) impacts the outcome of the analysis. For more information, please see the Community article: Standardization in Cluster Analysis. If you intend to standardize your fields in your Clustering Model, you should select this option and the appropriate method here.
Next, you can pick your clustering method, either K-Means, K-Medians, or Neural Gas.
All of the options you have configured so far should correspond directly to what you intend to set for your clustering solution in the K-Centroids Cluster Analysis Tool. The next few configuration options are specific to the Diagnostics Tool.
First, you need to select the range of possible number of cluster values you’re interested in working with. The minimum number of clusters is by default set to 2. Anything lower would be pointless (why bother performing clustering analysis if you only want a single group for your data?) or impossible (what would half a cluster or a negative cluster look like?). The maximum number of clusters is by default set to 4, but you can increase it up to 70. The tool will create clustering solutions for each integer in your range. You will be able to assess the fit of each solution using the two metrics generated in the tool’s output report.
The Bootstrap replicates option determines the number of different random samples of your data (with replacement) and therefore the number of times each clustering solution (for each number of target clusters) will be repeated. Bootstrapping effectively creates multiple replicates of your training data, which can be leveraged to infer the uncertainty and confidence intervals associated with your dataset (or given clustering solution for a data set).
The default setting for bootstrap replicates is 50 (the minimum), and can be set as high as 200. There is a trade-off in the number of bootstrap replicates created. Setting the value as a higher number results in better accuracy, but will also cause exponential growth in processing time. There is a point of potential diminishing marginal return as the number of bootstrap replicates increases.
The number of starting seeds argument sets the number of repetitions (nrep) argument, which repeats the entire solution building process the specified number of times, and keeps only the best solution. This is a necessary argument due to the random nature of how the clustering algorithms are initiated. The first step is randomly creating points as initial centroids. The final solution can be impacted by where these initial points are created. It can be set as low as 1 and as high as 10.
The Graphic Options tab simply lets you configure the graphics components of the plot output with the R anchor. You can specify the size of your plot in inches or centimeters, as well as the Graph Resolution (in dots per inch) and the base font size (in points).
There is only one output for the K-Centroids Diagnostics Tool. It is a report that you can now use to determine the optimal number of clusters to create in your clustering solutions.
Now that we have the tool configured, and we can see our results, let’s talk about what the tool is actually doing, and how you might be able to go about interpreting the report.
Results
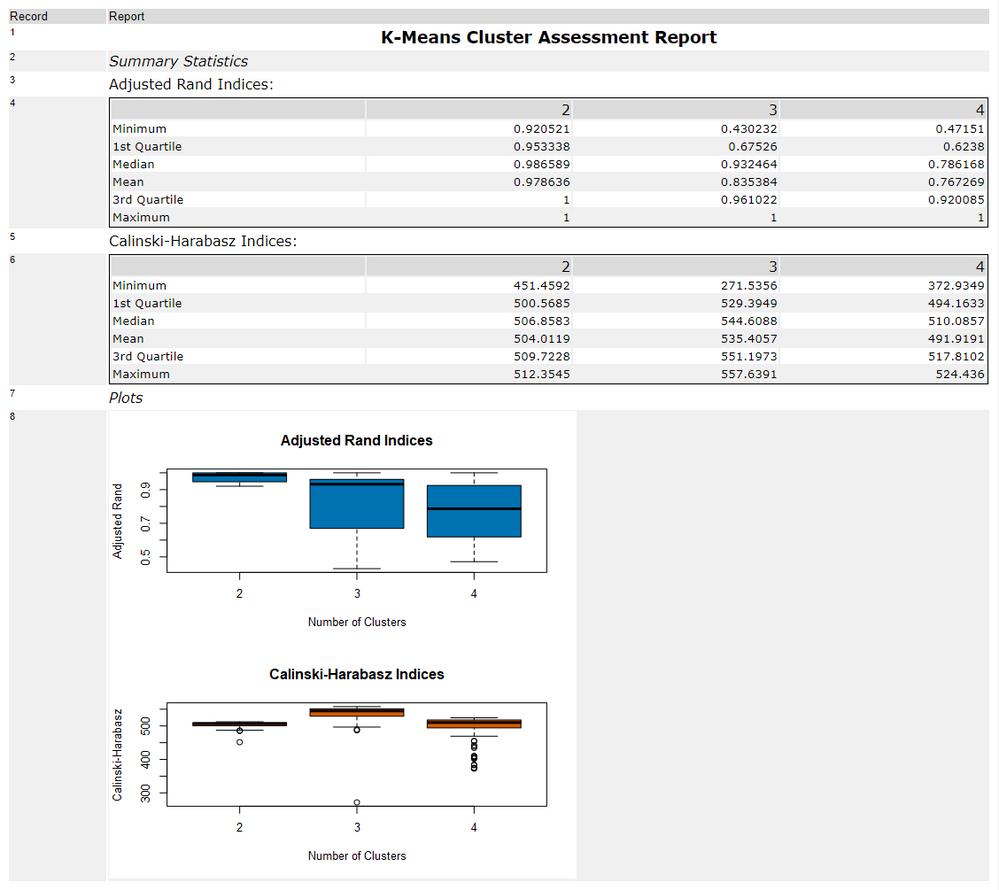
The K-Centroids Diagnostics Tool calculates two different statistical measures over bootstrap replicatesamples of the original data set, calculating these measures for the specified range of target clusters. The two statistical measures used for assessment, are the Adjusted Rand Index(also called the Ratio Criteria) and the Calinski-Harabasz Index (a.k.a. the pseudo f-statistic). The Adjusted Rand Index is a measure of similarity between two data clustering solutions, adjusted for the change grouping of elements. The Calinski-Harabasz Index is an internal measure of homogeneity and cluster separation (i.e., how “tight” the clusters are vs. how separated each cluster group is from one another). Additional description for both of these indices can be found inthis documentationfrom Bernard Desgraupes.
The report itself includes two representations of each of these metrics, a table and a box-plot. For each target cluster number, the index is calculated for all bootstrap replicates. The tables and plots report the indices of each of these trials as overall distributions.
The table is reported in quartiles,which highlight the overall distribution of the calculated values. The minimum Adjusted Rand and Calinski-Harabasz Indices are reported as the first row in the table, the middle value between the minimum and median (Q1), the median (Q2), and so on.
The box-plotsare a visualization of the distributions of index values across the bootstrap replicates (and clustering solutions). The second and third quartiles are depicted by the shaded box, the dashed lines display the spread of the first and fourth quartiles, and points indicate any outliers.
The Adjusted Rand Index is on a scale of 0 to 1, where 0 indicates totally random clusters. It is a measure of agreement between clustering partitions. Higher values indicate higher agreement.
For the Calinski-Harabasz Indices, higher values also indicate a better solution. The Calinski-Harabasz index tends to be most accurate when the clusters and approximately spherical in shape, and compact in the middle (i.e., normally distributed). This index all tends to prefer cluster consisting roughly of the same number of records.
As a rule, you are looking for the number of clusters where the index values are maximized, and the spread of the quartiles are minimized. In this example, two clusters seems to result in consistently high values for the Adjusted Rand Index, and three clusters has a high median, but at least one very low index value. The Calinski-Harabasz index shows that the 3-cluster solutions seem to have the higher values, although there is an low-value outlier.
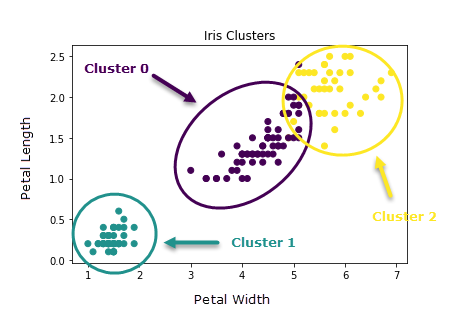
Given these results, in conjunction with what we know about the data, I would elect to use three clusters to create a solution.
I suspect the reason we see more consistent results with the two clustering solutions is due to the overlap between Iris-Versicolor and Iris-Virginica and the relatively distinct separation of Iris-Setosa.
In many ways, data science is as much of an art as it is an analytic process. Even with this tool, you may find you want to perform cluster analysis with the K-Centroids Cluster Analysis Tool multiple times per dataset, with many configuration variations.
By now, you should have expert-level proficiency with the K-CentroidsDiagnostics Tool! If you can think of a use case we left out, feel free to use the comments section below! Consider yourself a Tool Master already? Let us know atcommunity@alteryx.comif you’d like your creative tool uses to be featured in the Tool Mastery Series.
Stay tuned with our latest posts every#ToolTuesdayby following@alteryxon Twitter! If you want to master all the Designer tools, considersubscribingfor email notifications.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
@SydneyF Did you use Alteryx to create that last graph with the different colors for the clusters?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi @Kenda,
I am so glad to see you digging into cluster analysis with these articles! The last image in this article is a screenshot of a plot I developed using the Python Tool and then annotated (added the circles, arrows, and cluster labels) with my screenshot software. Very similar code is demonstrated in the Python Tool | Tool Mastery on Community.
Thanks!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Good afternoon,
Is there a way to set the seed value before running the diagnostic tool to ensure reproducible results?
Thanks,
Ray
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi @rmboaz,
There is not currently a way to set a seed for the K-Centroids diagnostics tool. If this is a feature you would like to see added, please consider posting to our ideas forum.
Thanks,
Sydney
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi,
The tool is able to indicate outliers for each of the "number of clusters", but is it possible to actually identify these outliers? And omit these data points accordingly?
Thanks
afk
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi @akasubi,
The K-Centroids Diagnostics tool works by performing cluster analysis on many different bootstrap replicates of the original data set, and then evaluating the cluster analysis with two different metrics. The goal of the tool is to help guide how many clusters will work best for a given data set. The outliers depicted by the box-plots are "trials" where the clustering analysis was particularly effective or performed particularly poorly for the given bootstrapped sample of data points. All of this is to say, the outliers are not outliers in the data set being analyzed - they are outliers in performance of clustering analysis for a given number of clusters.
If you are trying to identify outliers in your data set, I recommend looking into the data investigation tools. You might also find this thread helpful.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Thank you for this excellent write-up which is very helpful for learning the Predictive Group Tools.
-
2018.3
1 -
2023.1
1 -
API
2 -
Apps
7 -
AWS
1 -
Configuration
4 -
Connector
4 -
Container
1 -
Data Investigation
11 -
Database Connection
2 -
Date Time
4 -
Designer
2 -
Desktop Automation
1 -
Developer
8 -
Documentation
3 -
Dynamic Processing
10 -
Error
4 -
Expression
6 -
FTP
1 -
Fuzzy Match
1 -
In-DB
1 -
Input
6 -
Interface
7 -
Join
7 -
Licensing
2 -
Macros
7 -
Output
2 -
Parse
3 -
Predictive
16 -
Preparation
16 -
Prescriptive
1 -
Python
1 -
R
2 -
Regex
1 -
Reporting
12 -
Run Command
1 -
Spatial
6 -
Tips + Tricks
1 -
Tool Mastery
99 -
Transformation
6 -
Visualytics
1
- « Previous
- Next »