Tool Mastery
Explore a diverse compilation of articles that take an in-depth look at Designer tools.- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Tool Mastery
- :
- Tool Mastery | Linear Regression
Tool Mastery | Linear Regression
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
11-03-2016 03:45 PM - edited 08-03-2021 01:01 PM

If you're using the Linear Regression Tool in v11.0+, be sure to familiarize yourself with the tool's redesign!
Linear regressionis a statistical approach that seeks to model the relationship between a dependent (target) variable and one or more predictor variables. It is one of the oldest forms of regression and its applications throughout history have been endless for modeling all kinds of phenomena. In linear regression, a line of best fit is calculated using the least squaresmethod. This linear equation is then used to calculate projected values for the target variable given a set of new values for the predictor variables.
In Alteryx we have a linear regression tool that is actually an R based macro. It may look intimidating at first but it is actually very easy to configure. You simply select the target variable as well as the predictor variables in your dataset. You can also select whether or not you want to omit a model constant and/or use a weight variable for weighted least squares. After you have run your regression, two things will be outputted: The model object and a results report, which goes into statistical details of the generated least squares regression line.
The model object is outputted from the R tool inside the linear regression macro. This model object can be used as an input for three different tools in the predictive category (Nested Test, Score, and Stepwise).
- TheNested Test Tooldoes a model comparison to see if removing and adding variables to another Linear Regression tool significantly changes the predictive capabilities of the model.
- TheScore Tooluses the regression line obtained from the Linear Regression tool and calculates the new values for the target variables based on the values from the predictor variables being fed into the tool.
- TheStepwise Toolis for determining the optimal predictor variables to include in your model out of all potential predictor variables.
As mentioned above, the results output gives you a summary of how your model performed. For the sake of length here, we will not go into major detail of each and every component of this summary. If you still need further explanation of the statistics posted in the report we recommend seeking out additional resources to expand your knowledge (courses, Google, YouTube,Alteryx’s Udacity class, etc…) In the report we see:
- The numbers from aboxplot of the residuals
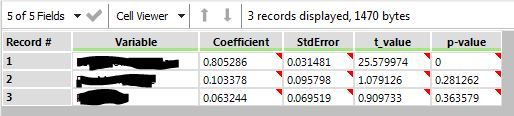
- Estimated model coefficients as well as their associatedP, t, and standard error values.
- RSE,R-Squared,F-statisticfor the regression line
- Type II ANOVA Analysisfor the variables
Now that we know what to expect from this tool, let’s go into different ways we can utilize the Linear Regression Tool.
Note: Before performing any predictive analysis it is imperative that the user be familiarized with the data they are feeding into the predictive tools. Data Investigation tools such as theField Summary Toolmake it easier to see what the data looks like to see if there are missing values, nulls, or a bunch of zeros that might cause the tools to error out. SeeTroubleshooting the Predictive Toolsif you are getting errors from this tool.
- Simple linear regression
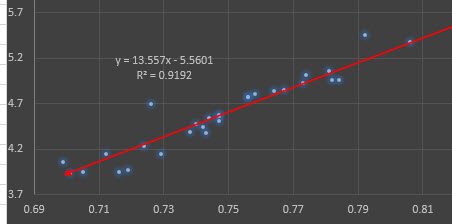
This is for bivariate data (one predictor variable and one target variable). For Excel users that are used to highlighting two fields and making a scatterplot or using theregression tool analysis in Excelto obtain your regression line, this should look familiar to you.
In this case, instead of seeing the equation in y=mx+b format, your slope (predictor variable coefficient) and intercept are going to appear here in the Results Output.
Tips: The assumptions you’re making before running this tool is that your variables have some correlation and that a change in the input variable can be expected to cause a uniform change in the output variable. It might be a good idea to perform an Association Analysis to see if this is the case; if the two variables are not correlated at all then linear regression might not hold any value. Also, ask yourself whether one predictor variable is enough to accurately predict the target variable
- Multiple Linear Regression
This when you are feeding in more than one predictor variable in your linear regression. All that changes here in terms of the output will be a longer list of coefficients for your variables, as well as the list for Type II ANOVA analysis. Unlike simple linear regression, there are a lot more things to watch out for in multiple linear regression.
Tips: Adjusted R^2 is more important than R^2; the more variables you throw into the inputs without substantively improving the R^2, the smaller the adjusted R^2 gets. Also be mindful of multicollinearity with the predictor variables you choose. A simplified model can often do better than one with too many input variables.
- Exponential Regression and Power Regression
The great thing is we can also use the linear regression tool to perform exponential regression and power regression. So for all those relationships that are more suited to be fitted with an exponential curve, like bank balance after compound interest (exponential growth), drug in your body over time (exponential decay) or even as something as complex as theinitial mass functionof stars (power law),we can still perform linearregression. How’s that, you may ask? Well, we can transform the target variables and/or predictor variables to make the relationships become linear.
Forexponential relationships, we can just simply take the natural log of your target variable in the formula tool before the Linear Regression tool. What is great is that the Score tool has an option that asks whether or not the target variables were transformed via the natural log. This means that you won’t have to do raise the outputs to the power ofeafter the Score Tool.
Forpower regressionwe take the natural log of both the target variable and predictor variable.
Hopefully this article has given you the courage and power to try linear regression on your data. If you're still feeling uneasy or are more of a visual learner like myself, check out these two resources:
- Asample tutorialfrom our YouTube channel.
- Predictive analytics starter kitfrom the Alteryx gallery, as it provides you with a full walkthrough of an example of using linear regression.
If you enjoyed this topic and want to learn more about predictive capabilities within Alteryx, check out the One Stop Shop for Predictive Resourcesor our Community Live Training video on Regression Modeling!
By now, you should have expert-level proficiency with the Linear Regression Tool! If you can think of a use case we left out, feel free to use the comments section below! Consider yourself a Tool Master already? Let us know at Community@alteryx.com if you’d like your creative tool uses to be featured in the Tool Mastery Series.
Stay tuned with our latest posts every Tool Tuesdayby following Alteryxon Twitter! If you want to master all the Designer tools, consider subscribingfor email notifications.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi Fredrick,
You could adjust the precision but that would involve going into the linear regression macro and changeing some of the R code.
-Ozzie
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Is there a way to save regression coefficients into a variable
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
@marinaurs,
The Model Coefficient macro available in the gallery outputs coefficients from the regression tool.
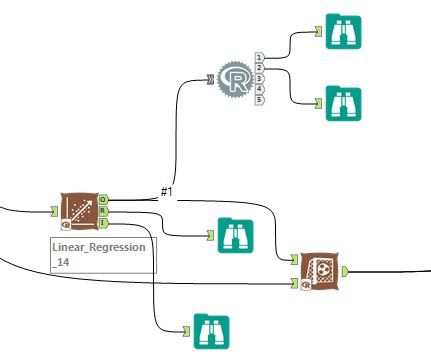
I have used R code in this solved question about linear regression and the R tool to do the same thing. It comes with grave warnings to be careful what you do with the coefficients and what calculations you do next. Instead, you can just use the Score tool to connect to the output of the linear regression tool to use the model. (here I have done both while checking the results of my work.)
Code in R tool:
Output of R tool 1:
Output of R tool 2:
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Is there a way to force the intercept to 0?
so manually we can have 0 intercep linreg this way (edit the macro's R tool)
cars.lm <- lm(dist ~ speed, data = cars) cars.lm2 <- lm(dist ~ 0 + speed, data = cars) summary(cars.lm)
# Adding the 0 term tells the lm() to fit the line through the origin
So a minor addition of a tickbox will solve that i guess... Best...
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Alteryx training is better than most Masters' Degrees.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
How do you download the predictive tools? I logged into Alteryx and got to the licensing field, but I do not know which package to download to get the Linear Regression tool.
From here, how do I download the predictive tools?
Your help is appreciated.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
@Sheahana
Select Alteryx Designer, then find the version of Designer (or Server) you're running in the tabs (New Version or Previous Versions). There you'll be able to download the matching RInstall file. (If the specific build you're using is no longer available, that is an indication that there were bug fixes released since you installed, so you probably want to upgrade your copy of Designer to the sub-version that is available.)
-
2018.3
1 -
2023.1
1 -
API
2 -
Apps
7 -
AWS
1 -
Configuration
4 -
Connector
4 -
Container
1 -
Data Investigation
11 -
Database Connection
2 -
Date Time
4 -
Designer
2 -
Desktop Automation
1 -
Developer
8 -
Documentation
3 -
Dynamic Processing
10 -
Error
4 -
Expression
6 -
FTP
1 -
Fuzzy Match
1 -
In-DB
1 -
Input
6 -
Interface
7 -
Join
7 -
Licensing
2 -
Macros
7 -
Output
2 -
Parse
3 -
Predictive
16 -
Preparation
16 -
Prescriptive
1 -
Python
1 -
R
2 -
Regex
1 -
Reporting
12 -
Run Command
1 -
Spatial
6 -
Tips + Tricks
1 -
Tool Mastery
99 -
Transformation
6 -
Visualytics
1
- « Previous
- Next »