Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Re: Challenge #18: Predicting Baseball Wins
Challenge #18: Predicting Baseball Wins
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I will be at Inspire! Let's definitely meet up!! I'll send you a message :)
NJ
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
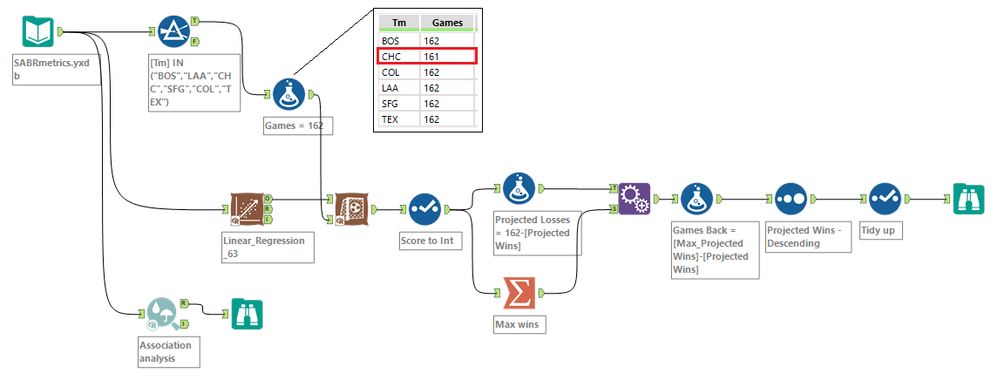
Here's my solution. I spotted an anomaly in the dataset in that CHC has 161 games historically but we're asked to assume 162 games for the prediction. I corrected it using a formula tool but it actually makes no difference at all to the scores (even when you look to multiple decimal places). Interesting!
**EDIT: Thinking about this, Games isn't included in the model so why would it make a difference anyway? Eh Jamie? What were you thinking? Anyway, I'll do the right thing and leave this here as a memorial to that one time I got it wrong.**
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This was a challenge that I burned too many brain cells over, for sure.
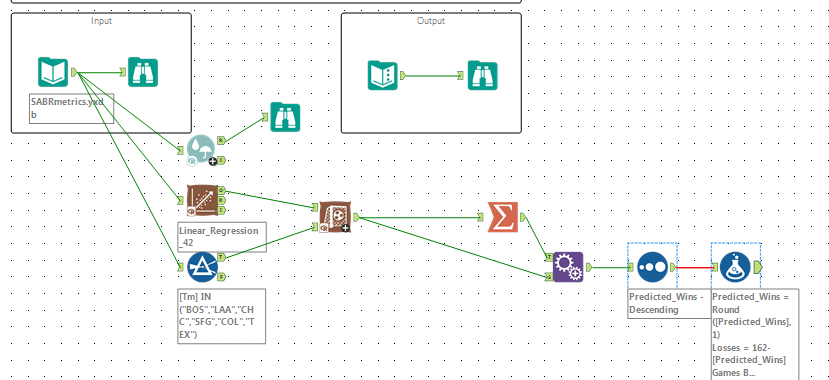
UPDATE: I challenged Alteryx and myself to find a better solution than a multivariate linear regression model, so I've included tests of five separate supervised algorithms and used the model comparison tool to select the best model. The winner was the Neural Net using the three principal components. There are advantages to using PCA results with neural nets, as can be found in an answer here: https://stats.stackexchange.com/questions/67986/does-neural-networks-based-classification-need-a-dim.... The neural net model has a mean absolute error of LT 2, which is both fantastic and raises some skepticism that it's overfitting and even memorizing the data, and the root mean squared error is still 2 1/2x less than the Random Forest model to almost 4x less than any other model.
The team statistics are normally distributed, a plus. But, there are a lot of highly correlated attributes as baseball statistics are a mix of raw compilations and computed statistics; for example, OPS is On-base Percentage (OBP) + Slugging Percentage (Slug). Highly correlated variables create collinearity, which makes regression models freak out by making some variables more important or less important than they should be. There are a number of ways to handle highly correlated predictor variables, but to follow this challenge's directions I highlighted the top 10 variables (which as a data scientist I would not do), and then I noted that those variables created collinearity; for example, Runs and Runs per Game are really the same and highly correlated with one another. I handled this problem by creating principal components, and found that 2 PCs accounted for 93+% of the variance within the data, an incredibly high coverage.
My wins predictions are somewhat different from most other solutions, but I believe this is true because my regression model's R-squared of 0.3726 and adjusted R-squared of 0.3002 indicate the reduced collinearity created by the tightly correlated top 10 variables, where other solutions indicated results of an R-squared of 0.5571 and adjusted R-squared of 0.3241, indicative of an internal collinearity issue due to the adjustment. The model is confused as to which variables are the real indicators of predicted wins.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
-
Advanced
302 -
Apps
27 -
Basic
158 -
Calgary
1 -
Core
157 -
Data Analysis
185 -
Data Cleansing
5 -
Data Investigation
7 -
Data Parsing
14 -
Data Preparation
238 -
Developer
36 -
Difficult
87 -
Expert
16 -
Foundation
13 -
Interface
39 -
Intermediate
268 -
Join
211 -
Macros
62 -
Parse
141 -
Predictive
20 -
Predictive Analysis
14 -
Preparation
272 -
Reporting
55 -
Reporting and Visualization
16 -
Spatial
60 -
Spatial Analysis
52 -
Time Series
1 -
Transform
227
- « Previous
- Next »