General Discussions
Discuss any topics that are not product-specific here.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- General
- :
- Re: Advent of Code 2022 Day 11 (BaseA Style)
Advent of Code 2022 Day 11 (BaseA Style)
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Adding modular arithmetic to my list of math to study for fun someday
Workflow:

Iterative macro:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
split item to rows and
use dynamic replace function to evaluate the operation easier for random input.workflow:
macro:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finally had the time to sit down and finish off day 11 - found this one really fun... even if I did spend ages trying to diagnose my calcs, only to realise I was doing 1k iterations instead of 10k!
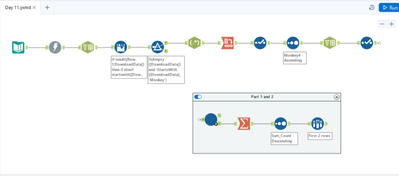
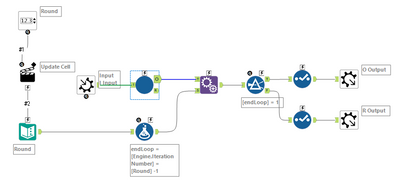
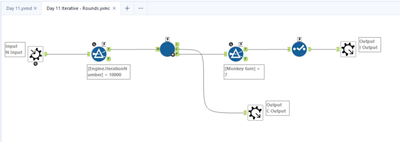
'Rounds' iterative:
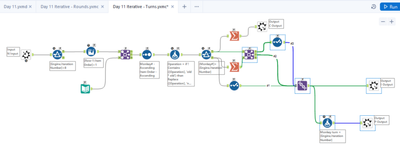
'Turns' iterative:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So - only 11 days late, part 2 of day 11 is finally solved. It took about 4 hours to run, and is kinda messy but it's solved. This one is tricky because it's not just a coding challenge, you need to think about the fundamental math involved (not complex math).
This took a long time for 2 reasons:
- Day 1 only took a few hours.
- lost 3 days trying out different ideas to combat the very-large-number issue in day 2 - by the end of day 3 I had a proof of the method that would work
- then lost a few days with work
- When I finally got down to it - it was only about 3 hours of work to get this done.
Below is the dirty solution - I'll clean this up when I do the refactoring.
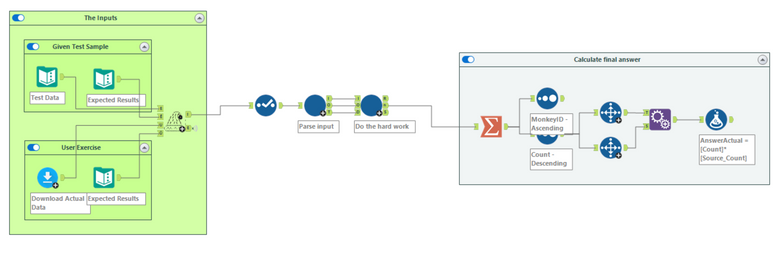
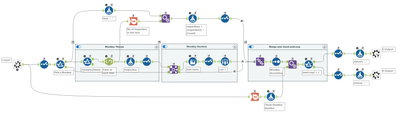
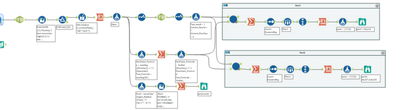
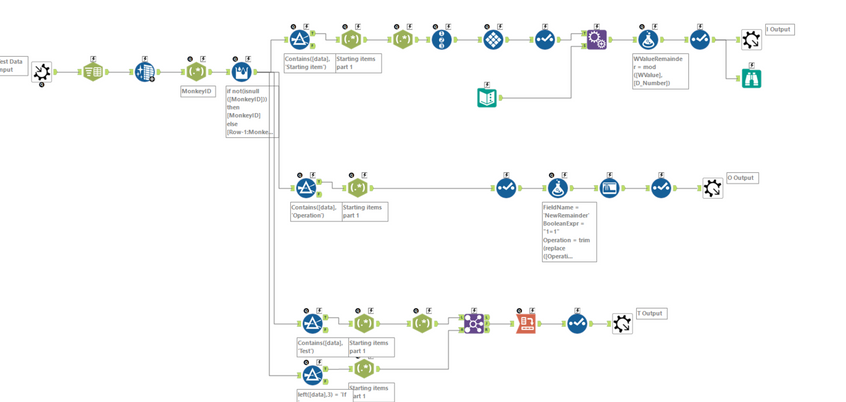
the work gets done in 2 main places - the parser and the solver.
The parser takes the input and generates 3 outputs.
- One is the items and the monkeys - this way you get a list of items associated with each Monkey with a unique ID on each.
- the second is the operation that is done - e.g. multiply by 19
- the third is the decision criterion about when to change monkeys - e.g. if divisible by 23 then Monkey 2 else Monkey 3
As you can see by the number of green tools - this is largely a parsing exercise - not trivial but not too tough - more just messy.
The next part is the solver. This has 3 layers:
Layer 1: Iterate for every round, and stop when the round limit is reached
Layer 2: Within this round - iterate for every item that is moved until all monkeys have been dealt with
Layer 3: Make 1 move for 1 monkey for 1 item
Here are the 3 layers:
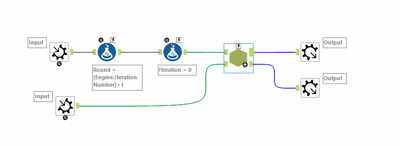
Layer 1: Round by Round iterator:
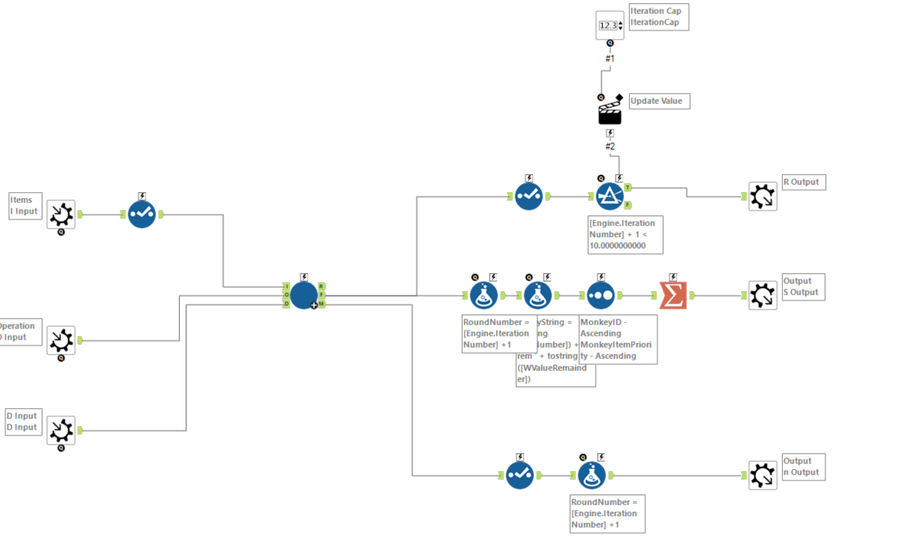
Nothing all that fancy here - just running htrough every round, passing them through to the one that moves by monkey - and adding an iteration number and trapping for the iteration cap.
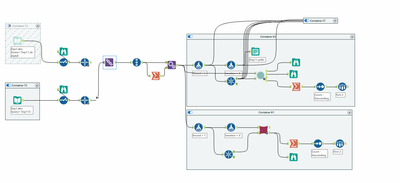
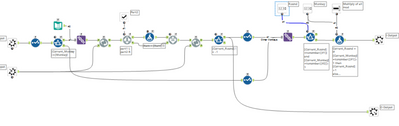
Layer 2: Within Round Iterator
This does look a bit messy - but what it's doing is going through the items with a Monkey in an order so that you don't keep on going round again and again - and so that if something is allocated to an earlier Monkey then this is left to Layer 1 to process in a later round. Again - messy but not too rough once you get your head round it.
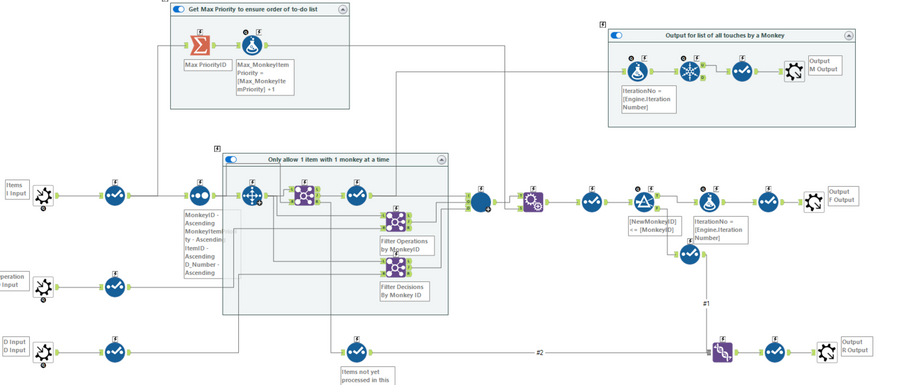
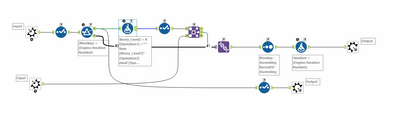
Layer 3: 1 Monkey 1 throw:
This is where the complexities lie.
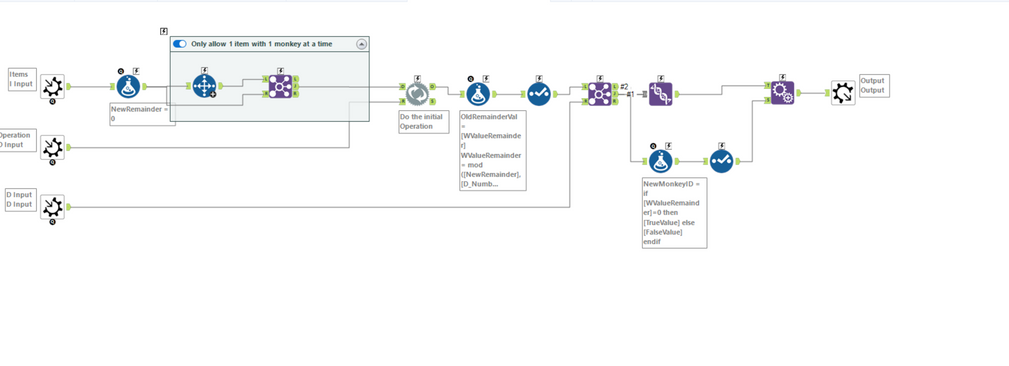
Firstly - every throw requires a dynamic formula because you have to do a different operation - so used a Dynamic Replace which takes a little bit of work to get comfortable with.
Then - to deal with the large numbers you need to change the way you think a little.
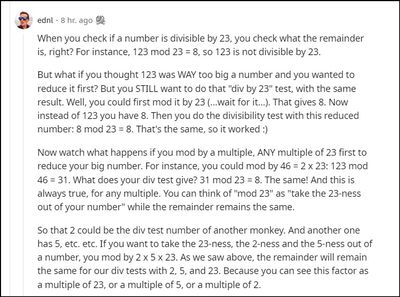
Instead of focussing on the number itself (which keeps on getting bigger and bigger and bigger) - instead focus on the remainders when a number is divided by X.
If you notice - all the "divisible by" numbers are all primes - so you can set up your data so that you store a list of "what is the remainder when I divide by 9; 13; 17" etc.
The fun thing about remainders is that if you have a number and multiply it by 10 - the remainder when dividing by 13 also multiplies by 10.
e.g. number is 15. 15 mod 13 is 2.
Now if you multiply 15 by 10 - you get 150. If you want to figure out the remainder when dividing by 13 - just take the original remainder, multiply by 10; eliminate multiples of 13 and you're done.
so 2* 10 = 20
20 mod 13 is 7
So: 150 mod 13 is also 7.
this becomes obvious if you think about the number 15 as ax+b type structure.
- So 15 is 1x13 + 2
- if you multiply 15 by 10 - then you get (1x13 + 2) * 10
- which is 1x13x10 + 2x10
- which is 10x13 + 20
- we know that 10x13 is divisible by 13, so no need to store this - the only interesting number is 20
- now 20 is 1x13 + 7
- which means that 15x10 now equals (10x13 + 1x13 + 7)
- or... 11x13 + 7
or remainder 7
So the trick here is - do the same operation on the remainders for each of the prime numbers up to ~23 or so - and you don't have to store the very big numbers if you want to know which Monkey to send it to.
- « Previous
-
- 1
- 2
- Next »
-
.Next
1 -
2020.4
1 -
AAH
3 -
AAH Welcome
8 -
ABB
1 -
Academy
222 -
ADAPT
9 -
ADAPT Program
1 -
Admin
1 -
Administration
2 -
Advent of Code
135 -
AHH
1 -
ALTER.NEXT
1 -
Alteryx Editions
4 -
Alteryx Practice
442 -
Analytic Apps
6 -
Analytic Hub
2 -
Analytics Hub
4 -
Analyzer
1 -
Announcement
73 -
Announcements
25 -
API
3 -
App Builder
9 -
Apps
1 -
Authentication
3 -
Automation
1 -
Automotive
1 -
Banking
1 -
Basic Creator
5 -
Best Practices
3 -
BI + Analytics + Data Science
1 -
Bugs & Issues
1 -
Calgary
1 -
CASS
1 -
CData
1 -
Certification
270 -
Chained App
2 -
Clients
3 -
Common Use Cases
3 -
Community
814 -
Computer Vision
1 -
Configuration
1 -
Connect
1 -
Connecting
1 -
Content Management
4 -
Contest
46 -
Contests
1 -
Conversation Starter
159 -
COVID-19
15 -
Data
1 -
Data Analyse
2 -
Data Analyst
1 -
Data Challenge
185 -
Data Connection
1 -
Data Investigation
1 -
Data Science
102 -
Database Connection
1 -
Database Connections
3 -
Datasets
3 -
Date type
1 -
Designer
1 -
Designer Integration
4 -
Developer
5 -
Developer Tools
2 -
Directory
1 -
Documentation
1 -
Download
3 -
download tool
1 -
Dynamic Input
1 -
Dynamic Processing
1 -
dynamically create tables for input files
1 -
Email
2 -
employment
1 -
employment opportunites
1 -
Engine
1 -
Enhancement
1 -
Enhancements
2 -
Enterprise (Edition)
2 -
Error Messages
3 -
Event
1 -
Events
107 -
Excel
1 -
Feedback
2 -
File Browse
1 -
Financial Services
1 -
Full Creator
2 -
Fun
153 -
Gallery
2 -
General
23 -
General Suggestion
1 -
Guidelines
13 -
Help
72 -
hub
2 -
hub upgrade 2021.1
1 -
Input
1 -
Install
2 -
Installation
4 -
interactive charts
1 -
Introduction
25 -
jobs
2 -
Licensing
3 -
Machine Learning
2 -
Macros
3 -
Make app private
1 -
Marketplace
8 -
Maveryx Chatter
12 -
meeting
1 -
migrate data
1 -
Networking
1 -
New comer
1 -
New user
1 -
News
26 -
ODBC
1 -
Off-Topic
125 -
Online demo
1 -
Output
2 -
PowerBi
1 -
Predictive Analysis
1 -
Preparation
3 -
Product Feedback
1 -
Professional (Edition)
1 -
Project Euler
18 -
Public Gallery
1 -
Question
1 -
queued
1 -
R
1 -
Reporting
1 -
reporting tools
1 -
Requirements
1 -
Resource
117 -
resume
1 -
Run Workflows
10 -
Salesforce
1 -
Santalytics
9 -
Schedule Workflows
6 -
Search Feedback
76 -
Server
2 -
Settings
2 -
Setup & Configuration
5 -
Sharepoint
2 -
Starter (Edition)
1 -
survey
1 -
System Administration
4 -
Tax & Audit
1 -
text translator
1 -
Thursday Thought
57 -
Tips and Tricks
6 -
Tips on how to study for the core certification exam
1 -
Topic of Interest
167 -
Udacity
2 -
User Interface
2 -
User Management
5 -
Workflow
4 -
Workflows
1
- « Previous
- Next »