General Discussions
Discuss any topics that are not product-specific here.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- General
- :
- Advent of Code 2021 Day 15 (BaseA Style)
Advent of Code 2021 Day 15 (BaseA Style)
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does the path taken can be behave like snake game? U turns? Up-down?
I tried with define steps from 0,0, then calculate minimum sum needed to get to next step from previous, so going through the grid with a downward diagonal line (like Dijkstra), but answer is a bit off.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This works for part 1 in under 10 seconds, we'll see how long part 2 takes, assuming it finishes (I'm currently at 8 minutes and it slows down the farther it goes...so it may take hours to finish). I may need to try something different for part 2 to help it finish faster.
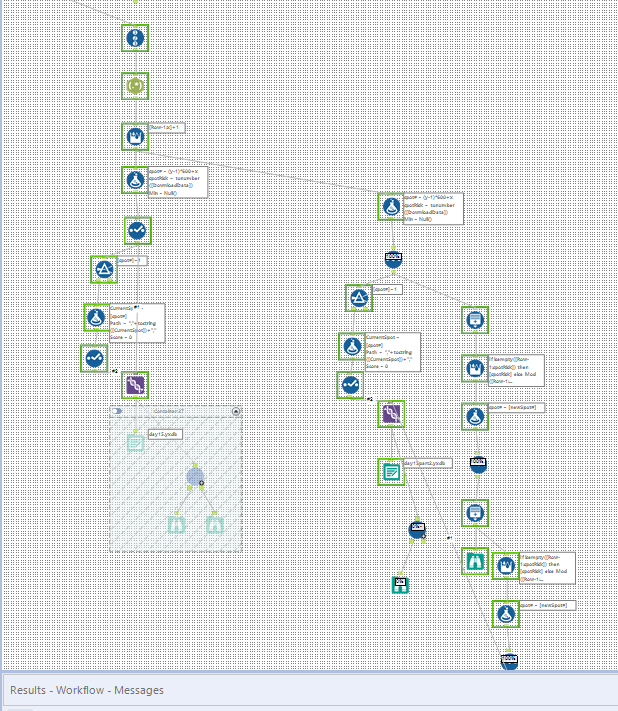
Super messy Macro:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Epic fail on part 2 (it may have never ended), so I reworked it for speed. I don't like it as much as my original logic, but part 2 now completes in <10 minutes. I also just relied on manually updating the number of iterations.
Iterative Macro:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fast this was not.
If any path reaches to the exit, use the minimum cost of exit to prune other paths in the next iteration. Keep doing this while we are visiting new cells in any path.
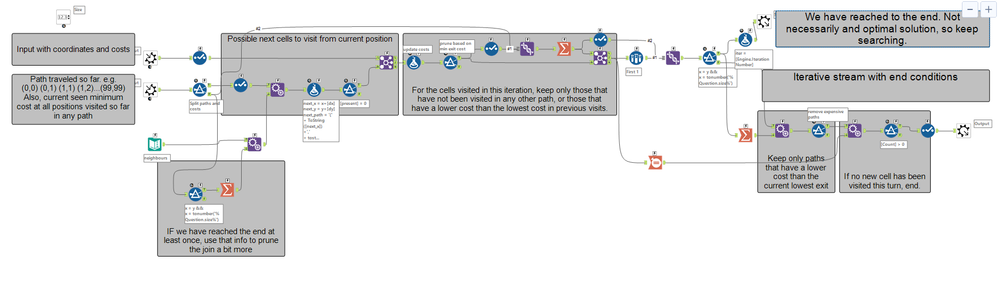
it "just" took it 1003 iterations to find the lowest cost, and 1010 iterations to complete (or 27 min!)
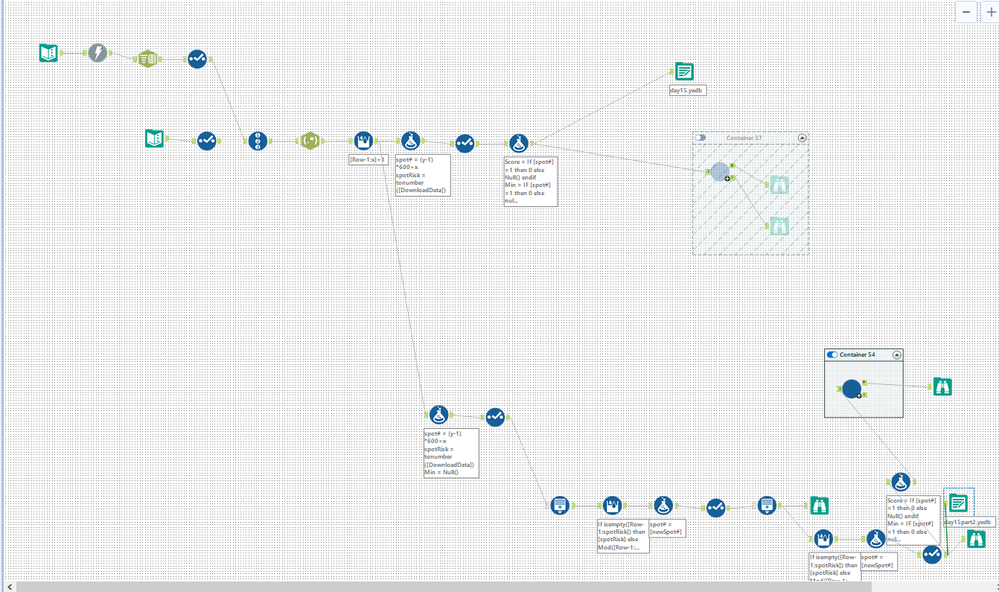
The main wf

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I didn't manage to complete Part 2 in 10 mins like @patrick_digan - mine came in at 1 hr 31 mins.
This one took 2 days to do cleanly - many different things came into play
- discovered and logged 2 defects
- spent WAY too much time looking into an issue where I'd used a max value which was too small
- overrun on Byte type integers (needed int16)
- instead of looping 1 at a time - switched to doing things in bulk (why I didn't think of this up front is a bit embarrassing).
Anyway - finally got this done - 4 days later. Algo and solution below the spoiler break:
Also - wrapped this in discrete modules to make it cleaner, and make it easier to read - and also added a utility macro that converts the shortest path to a map (like they do on the AOC website).
Setup
- Create the basic list of cells in a vertical list (i.e. don't treat this as a table, create this as a long list) with the cell ID (similar to @patrick_digan - except I used (001, 001) as the ID, where he used a unique integer which I should have done too 'cause it would have been much faster)
- Do the multiplication of the grid - simple formula with 2 generate rows
- Then for each cell - figure out who are the neighbours of that cell on any side
- Set the total path cost and shortest path for the starting node (001, 001) to be 0, and (001, 001) respectively - and 999999 for all other cells (you'll see why later)
The working area:
- For each iteration - you start with a list of focus nodes. The first time round, the only focus node is (001, 001)
- Join to all neighbours of the focus node
- If the total path cost from this focus node to the neighbour node is shorter than you've ever seen before, then update the total path cost and shortest path for that particular node, and that becomes a focus for next iteration.
.... loop until you run out of focus nodes
The reason that this works is because you don't try to find the shortest path by brute-forcing every combination of (that would be so computationally expensive, that it's not practical for any large data set).
Instead, you are starting from (001, 001) and exploring the neighbours, and progressively finding the shortest path from start to the neighbour - and if any path is NOT shorter, then let's stop thinking about it.
There's variant in this in the way that we do Game algorithms - where you do min/max (mind the maximum scores for my moves, then find the minimum scores for my opponent's moves - and that way you make the search tree smaller and capable of being explored.
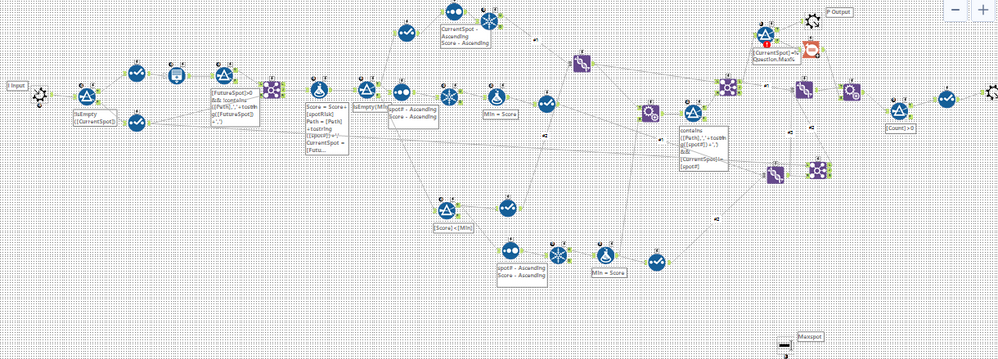
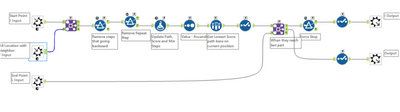
Here's the main flow, so that you can see the macro set up process and the main flow of logic:
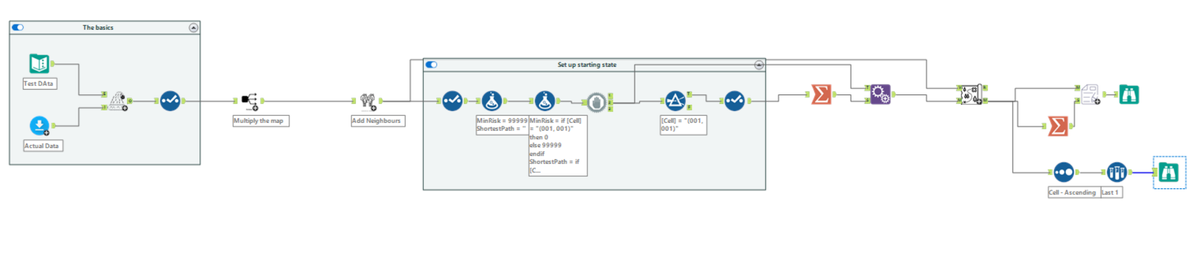
Then the shortest path map piece gets done in the module that looks like a map:

Again - based on the description of the Algo above, you should be able to see this reflected in the Alteryx canvas
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK - managed (with @patrick_digan 's suggestions) to get this down to 13m13 sec - details in the spoiler
- 1: Converted this to serializing the data onto the iteration stream - that didn't reduce the time - still ~1hr31m
- 2: Because I'd eliminated the files - I could now use AMP - AMP was failing because of a defect with Block until Done when using files. AMP brought this down to 31m37s - almost a 66% reduction. With this, all 16 cores were working hard at around 70% CPU, zero disk usage
- 3: Then got rid of the shortest path ( @patrick_digan suggestion) - this brought me down to 18m14sec - but curiously the CPU was now idling at around 17%
- 4: Removed all my debugging messages - took a few seconds off, now down to 18m flat - CPU now even more free at ~12%
- 5: Change from using cell IDs which were long strings "(001, 001)" to a single integer - this brought it down to 13m13s - CPU still taking an afternoon snooze at 14%.
Overall - I'm super interested in the fact that even with AMP engine turned on - I'm only really using a fraction of my CPU capacity - so what's taking the time? There's zero disk access - it's all coming from memory, and most of this should be the same data elements being hit again and again, so that should be coming into the L1/L3 cache. So why is Alteryx only hitting less than 1 in 5 CPU cycles?
Very interesting exercise!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This was a tricky one to conceptualise. I built something that worked with the test data fairly quickly but my sample had more paths so some debugging was required to output the right path without overloading my computer (a tale as old as time)
Part 2 I found pretty well with my old favourite Find and Replace<3.
Only took 7 hours because i messed up the risk limit calc so lots of unnecessary paths were calculated 😞
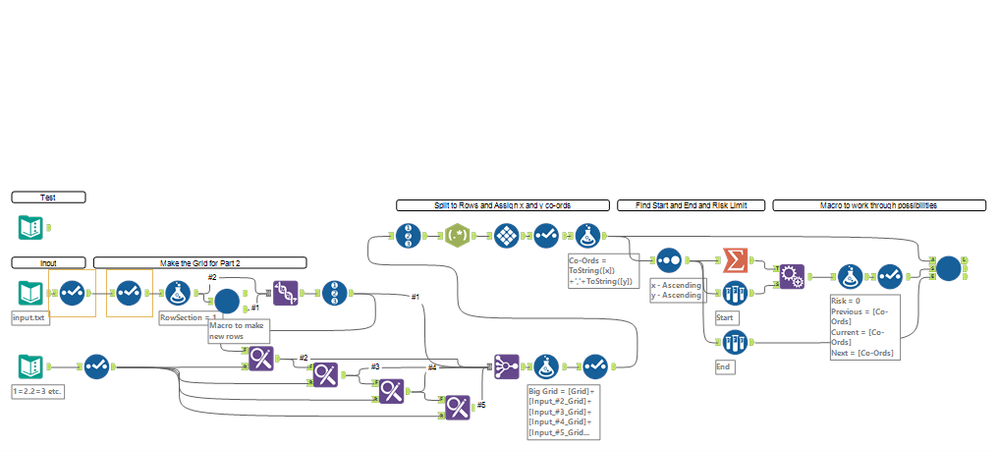
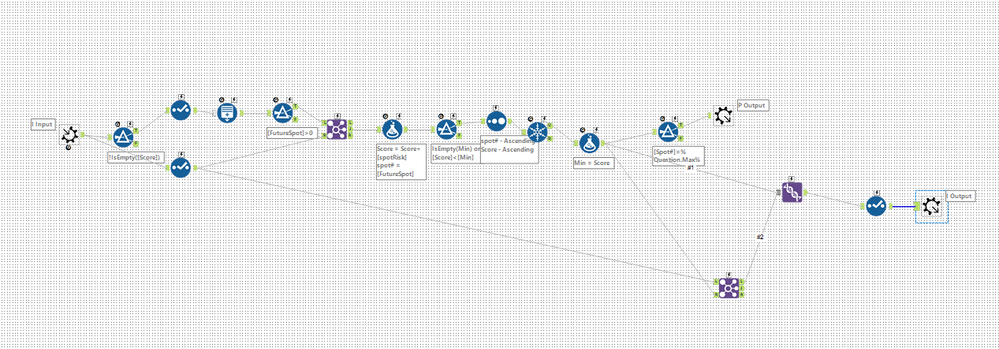
Macro to work out paths:
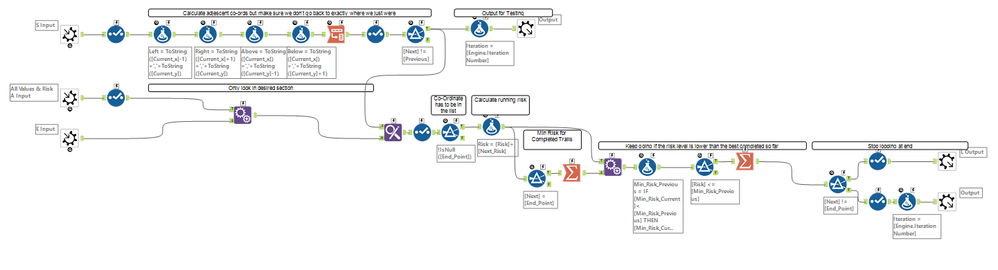
Macro to make 5x5 grid
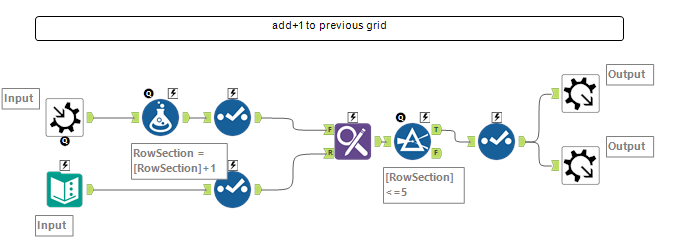
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks @patrick_digan
take for few days to solved part 1. On the way to part 2.
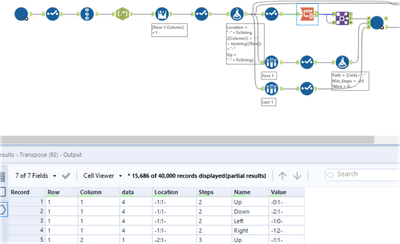
Keys learn from Patrick: when reach every point, only keep the lowest path.
for example: here have 2 paths that reach 2,2,
1,1 > 1,2 > 2,2 = 10
1,1 > 2,1 > 2,2 = 8
we only keep the 2nd as it is lowest.
by this way, it reduce Million records to max 40,000 records per iteration.
Workflow
surround location with "-" to avoid mistake in finding repeat path.
because i use contains to identity it. (like 1,10 is found in 11,10 and 1,100 etc)
steps = x + y.
mistake: forget to remove the start point value.
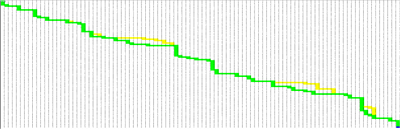
The Visual in excel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To enlarge 5 time without macro,
use generate row tool to add new row and column,
use formula to update the real row and column.
use mod to calculate the number can change 0 to 9.
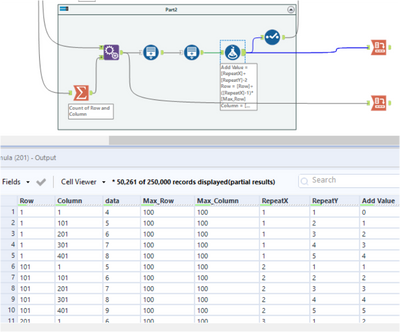
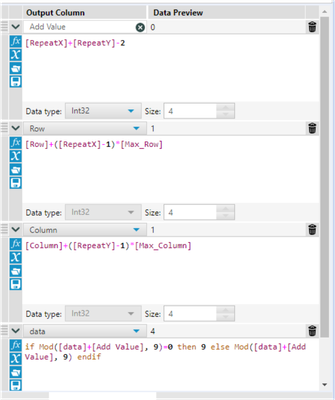
And macro is similar with above. but i add filter after the input of all possible macro, (base on the steps (i.e x + y) and iteration number) to reduce the times taken in join.
(i test on part 1, it reduce from 16 second to 13 second.)
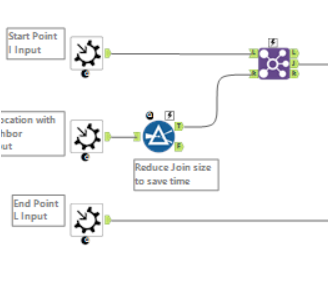
-
.Next
1 -
2020.4
1 -
AAH
3 -
AAH Welcome
8 -
ABB
1 -
Academy
222 -
ADAPT
9 -
ADAPT Program
1 -
Admin
1 -
Administration
2 -
Advent of Code
135 -
AHH
1 -
ALTER.NEXT
1 -
Alteryx Editions
5 -
Alteryx Practice
442 -
Analytic Apps
6 -
Analytic Hub
2 -
Analytics Hub
4 -
Analyzer
1 -
Announcement
73 -
Announcements
25 -
API
3 -
App Builder
9 -
Apps
1 -
Authentication
3 -
Automation
1 -
Automotive
1 -
Banking
1 -
Basic Creator
5 -
Best Practices
3 -
BI + Analytics + Data Science
1 -
Bugs & Issues
1 -
Calgary
1 -
CASS
1 -
CData
1 -
Certification
270 -
Chained App
2 -
Clients
3 -
Common Use Cases
3 -
Community
817 -
Computer Vision
1 -
Configuration
1 -
Connect
1 -
Connecting
1 -
Content Management
4 -
Contest
49 -
Contests
1 -
Conversation Starter
159 -
COVID-19
15 -
Data
1 -
Data Analyse
2 -
Data Analyst
1 -
Data Challenge
188 -
Data Connection
1 -
Data Investigation
1 -
Data Science
102 -
Database Connection
1 -
Database Connections
3 -
Datasets
3 -
Date type
1 -
Designer
1 -
Designer Integration
4 -
Developer
5 -
Developer Tools
2 -
Directory
1 -
Documentation
1 -
Download
3 -
download tool
1 -
Dynamic Input
1 -
Dynamic Processing
1 -
dynamically create tables for input files
1 -
Email
2 -
employment
1 -
employment opportunites
1 -
Engine
1 -
Enhancement
1 -
Enhancements
2 -
Enterprise (Edition)
2 -
Error Messages
3 -
Event
1 -
Events
110 -
Excel
1 -
Feedback
2 -
File Browse
1 -
Financial Services
1 -
Full Creator
2 -
Fun
156 -
Gallery
2 -
General
23 -
General Suggestion
1 -
Guidelines
13 -
Help
72 -
hub
2 -
hub upgrade 2021.1
1 -
Input
1 -
Install
2 -
Installation
4 -
interactive charts
1 -
Introduction
25 -
jobs
2 -
Licensing
3 -
Machine Learning
2 -
Macros
3 -
Make app private
1 -
Marketplace
8 -
Maveryx Chatter
12 -
meeting
1 -
migrate data
1 -
Networking
1 -
New comer
1 -
New user
1 -
News
26 -
ODBC
1 -
Off-Topic
125 -
Online demo
1 -
Output
2 -
PowerBi
1 -
Predictive Analysis
1 -
Preparation
3 -
Product Feedback
1 -
Professional (Edition)
2 -
Project Euler
21 -
Public Gallery
1 -
Question
1 -
queued
1 -
R
1 -
Reporting
1 -
reporting tools
1 -
Requirements
1 -
Resource
117 -
resume
1 -
Run Workflows
10 -
Salesforce
1 -
Santalytics
9 -
Schedule Workflows
6 -
Search Feedback
76 -
Server
2 -
Settings
2 -
Setup & Configuration
5 -
Sharepoint
2 -
Starter (Edition)
2 -
survey
1 -
System Administration
4 -
Tax & Audit
1 -
text translator
1 -
Thursday Thought
57 -
Tips and Tricks
6 -
Tips on how to study for the core certification exam
1 -
Topic of Interest
167 -
Udacity
2 -
User Interface
2 -
User Management
5 -
Workflow
4 -
Workflows
1
- « Previous
- Next »

