Alteryx Designer Desktop Discussions
Find answers, ask questions, and share expertise about Alteryx Designer Desktop and Intelligence Suite.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- Designer Desktop
- :
- Re: Matching Transactions to a Single Total
Matching Transactions to a Single Total
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have a 2 sets of data that have individual transactions on one of the sets, and Sum Totals in the other. I'm looking for a way to match up the transactions to the correct total
This feels like an iterative macro, but i'm having trouble conceptualizing the correct way to do it:
Set 1:
| Transaction | RecordID |
| 616.66 | 1 |
| 112.14 | 2 |
| 392.63 | 3 |
| 56.11 | 4 |
| 111 | 5 |
| 336.78 | 6 |
| 1122 | 7 |
| 336.48 | 8 |
| 112.4 | 9 |
Set 2:
| Total | RecordID |
| 2759.91 | 1 |
the output should be that Transactions 1,2,3,7,8 sum up to match the Total...
- Labels:
-
Iterative Macro
-
Macros
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, this is a puzzler! The number of permutations you'll need to test through an iterative macro is potentially huge. Can you provide a slightly larger sample of the data, i.e. with more than one total to match?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting problem. This could be one of the weekly challenges!
It's true that the number of permutations could get big very fast. Fortunately, what you are really looking for is the number of combinations (a much smaller number). This is defined by: n!/[r!(n-r)!].
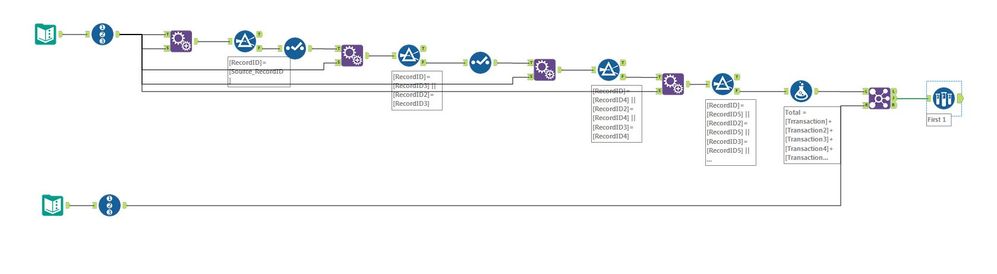
The thing you have to determine beforehand is the maximum number of transactions that can add up to your totals. Here's my attempt with the sample data you provided:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi all,
Thanks to JSNelson08 for submitting this - he was helping me with this project internally.
I ended up resolving this with nested macros. The outer macro is a batch macro that does the following, grouping by a field called "contract type" to reduce the data volumes:
1) Add record IDs to the set of records
2) Check to see whether the sum of all prices x quantities for this batch match. If so, don't pass anything to the inner macro, since we already know the total batch is matched.
3) Pass the unmatched items to the inner macro twice, since the macro takes one set of records as a constant and iterates on the other.
The inner macro is an iterative macro that first checks to see if any of its Right input match off against the Left, and if not, does a Cartesian join for its Right input to itself (i.e. creating a matrix of [price x quantity] xx [price x quantity] data, summing [price x quantity] and concatenating the record IDs with a comma delimiter). It then iterates on the joined output.
I had to put a couple of checks into the iterative macro to try to further reduce data volumes however I could. The big one was to take any [price x quantity] combinations that get matched out of the data set entirely, so that the iterative process wouldn't continue to balloon out on the records that already found their match.
Then the macros spit out the matched sets of record IDs and their prices x quantities, as well as anything that remains unmatched.
This was definitely a more difficult project than I anticipated when I was describing it to my office, and huge thanks to JSNelson08 for his help! Obviously this workflow can really start to chug if the data set gets too large, so I set the maximum iterations down to 3. It doesn't always match everything off as a result, but it still does a pretty solid job with most situations. The only ones that it can't match (assuming it SHOULD, i.e. our data set is valid and should be matchable) are sets where there are a large number of records coming through within a single "contract type" batch. I did a back of the envelope calculation assuming each record in the iterative macro (price x quantity, record id) was only 10 bytes, and for a 20-item set, the full Cartesian join is ~2.6MB. A 30 or 50-item batch will be too much for Alteryx to handle in a reasonable amount of time, so I just restricted the number of iterations and we deal with the resulting occasional failures to match as a manual procedure on the back end. This does save us a lot of time even with that limitation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hey @esmalley and @JSNelson08 ,
Thank you for this post, it is helping me with a current workflow I am trying to build to perform some reconciliation work. Is there any chance you may be able to share your nested macros that you used? It would be a great help to structure my approach on the work I am trying to do!
Many thanks!
-
Academy
6 -
ADAPT
2 -
Adobe
204 -
Advent of Code
3 -
Alias Manager
78 -
Alteryx Copilot
26 -
Alteryx Designer
7 -
Alteryx Editions
95 -
Alteryx Practice
20 -
Amazon S3
149 -
AMP Engine
252 -
Announcement
1 -
API
1,208 -
App Builder
116 -
Apps
1,360 -
Assets | Wealth Management
1 -
Basic Creator
15 -
Batch Macro
1,559 -
Behavior Analysis
246 -
Best Practices
2,695 -
Bug
719 -
Bugs & Issues
1 -
Calgary
67 -
CASS
53 -
Chained App
268 -
Common Use Cases
3,825 -
Community
26 -
Computer Vision
86 -
Connectors
1,426 -
Conversation Starter
3 -
COVID-19
1 -
Custom Formula Function
1 -
Custom Tools
1,938 -
Data
1 -
Data Challenge
10 -
Data Investigation
3,487 -
Data Science
3 -
Database Connection
2,220 -
Datasets
5,222 -
Date Time
3,227 -
Demographic Analysis
186 -
Designer Cloud
742 -
Developer
4,372 -
Developer Tools
3,530 -
Documentation
527 -
Download
1,037 -
Dynamic Processing
2,939 -
Email
928 -
Engine
145 -
Enterprise (Edition)
1 -
Error Message
2,258 -
Events
198 -
Expression
1,868 -
Financial Services
1 -
Full Creator
2 -
Fun
2 -
Fuzzy Match
712 -
Gallery
666 -
GenAI Tools
3 -
General
2 -
Google Analytics
155 -
Help
4,708 -
In Database
966 -
Input
4,293 -
Installation
361 -
Interface Tools
1,901 -
Iterative Macro
1,094 -
Join
1,958 -
Licensing
252 -
Location Optimizer
60 -
Machine Learning
260 -
Macros
2,864 -
Marketo
12 -
Marketplace
23 -
MongoDB
82 -
Off-Topic
5 -
Optimization
751 -
Output
5,255 -
Parse
2,328 -
Power BI
228 -
Predictive Analysis
937 -
Preparation
5,169 -
Prescriptive Analytics
206 -
Professional (Edition)
4 -
Publish
257 -
Python
855 -
Qlik
39 -
Question
1 -
Questions
2 -
R Tool
476 -
Regex
2,339 -
Reporting
2,434 -
Resource
1 -
Run Command
575 -
Salesforce
277 -
Scheduler
411 -
Search Feedback
3 -
Server
630 -
Settings
935 -
Setup & Configuration
3 -
Sharepoint
627 -
Spatial Analysis
599 -
Starter (Edition)
1 -
Tableau
512 -
Tax & Audit
1 -
Text Mining
468 -
Thursday Thought
4 -
Time Series
431 -
Tips and Tricks
4,187 -
Topic of Interest
1,126 -
Transformation
3,730 -
Twitter
23 -
Udacity
84 -
Updates
1 -
Viewer
3 -
Workflow
9,980
- « Previous
- Next »