How do you build a circle from 3 points?

[levonbjohnson]

I am looking for a way in Alteryx to find the latitude and longitude of the center of a circle that passes through three given points.

For example, let's say I have these three points:

Point	Latitude	Longitude
A	47.452335	-122.283136
B	47.420520	-122.238847
C	47.378923	-122.122804

I know the cartesian-plane math (using x and y coordinates) that would give me the center of the circle, but I do not know if it is even possile to simply convert the latitude/longitude to x/y coordinates as the Earth is not flat or even perfectly spherical (and the solution needs to work at both short and long distances where that would play a factor).

Ideally, I am hoping there is a method in Alteryx using Spatial tools to determine the latitude/longitude of the circle's center. Any help on this would be greatly appreciated (if this isn't possible, then any help on good ways to convert latitude/longitude to x/y coordinates that account for the non-spherical Earth would be the next best thing). Thanks!

[BenMoss]

Hi,

You could consider converting your points into a spatial polygon. To do this you would first need to create a  spatial object out of your latitude and longitude, to do this you can use the 'create points' tool. You could then use the 'polybuild' tool to create a spatial polygon, if you have multiple objects you want to create then you can use the group by option and select an identifier. I would use the 'convex hull' method which will not contain any concave angles, so it will never turn in on itself. If your points are in sequence then you could consider record IDing them and then using the 'sequence polygon' build method.

Once you have your spatial polygon you can thing use the 'spatial info' tool and find the centroid of the polygon by using the 'centroid as X and Y fields' option which will give the latitude and longitude of the centre of your object.

I hope this helps!

Ben

[RodL · Accepted solution]

The centroid of the polygon created by the 3 points doesn't get you the center of the circle (which is what is asked for), as evidenced by the centroid from the 3 points provided.

An interesting article that converts lat/long to Cartesian coordinates and then provides a formula to get the center of the circle can be found here...

http://mathforum.org/library/drmath/view/68373.html

Looks like you could build out the process going the steps outlined in the article.

[Hollingsworth · Accepted solution]

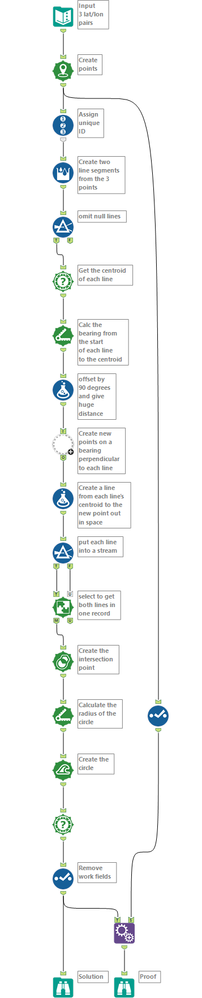
I solved this problem using the perpendicular math described in the solution but using only spatial tools.

See the attached package for the solution.