Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Challenge #67: Calculate Spatial Angles
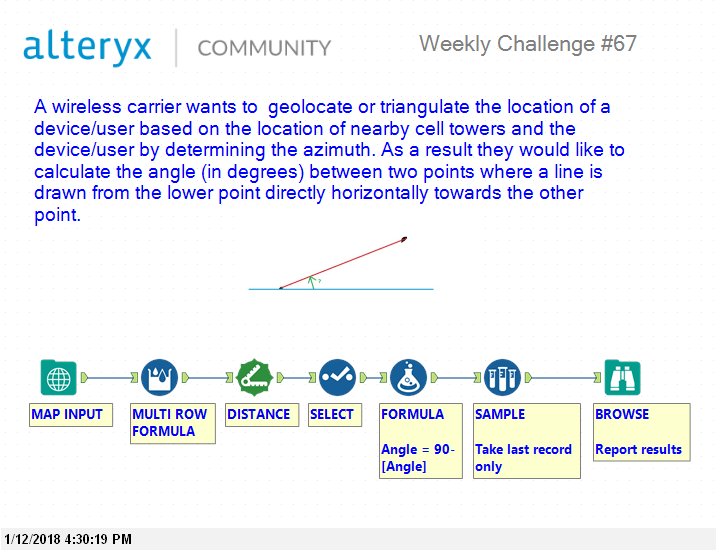
Challenge #67: Calculate Spatial Angles
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just realized there was a "bonus" part of the question. Will come back to it later.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
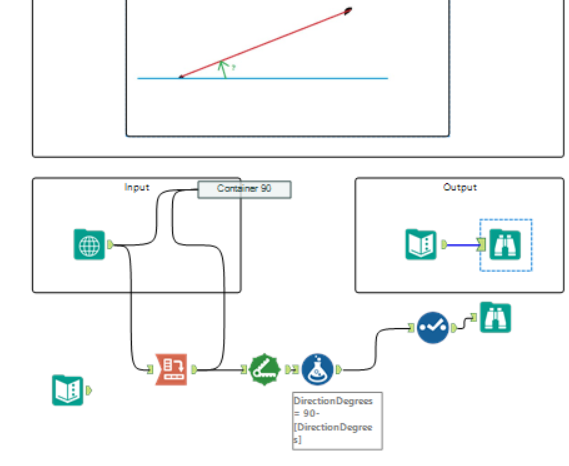
I solved this using the spatial tools (and a crowbar!) a couple of weeks ago but I left the non-spatial aspect of the challenge to come back to when I'd had more experience with Alteryx.
I now see my initial solution was needlessly over-complicated so I figured out a better way to do it, as well as solved the non-spatial tool method. I enjoyed working with the spatial expressions!
I left in my first pop at this challenge for everyone's amusement.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
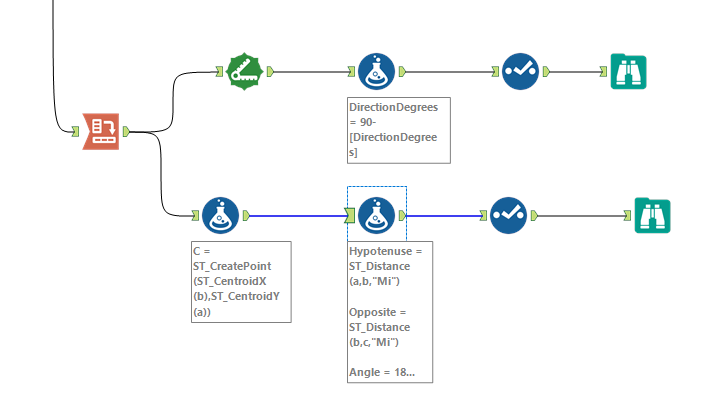
After much too much frustration over trigonometry and not remembering things, I finally figured it out. Moments after, I remembered the spatial tool that could so easily do this for me! So here are both ways.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
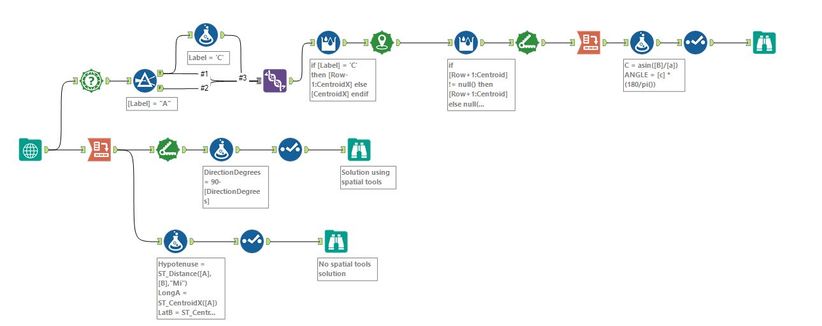
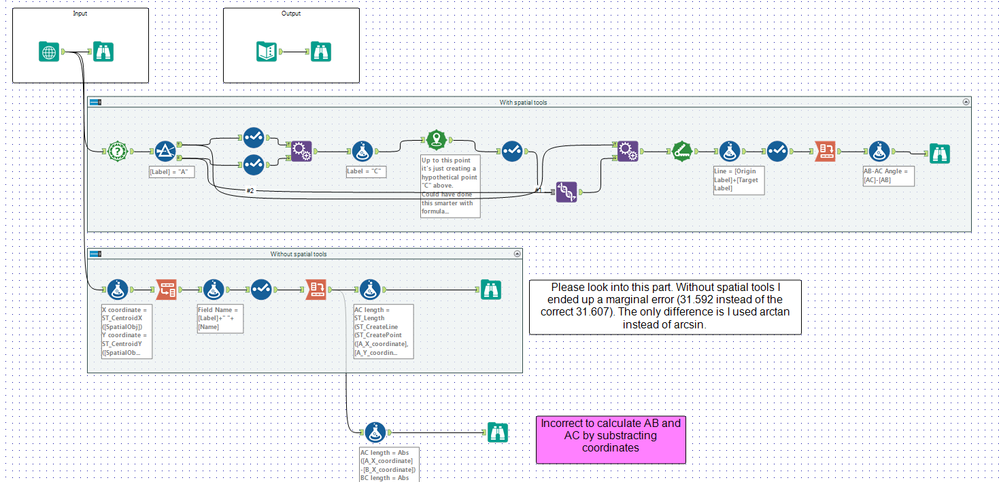
My workflow:
Illustrative:
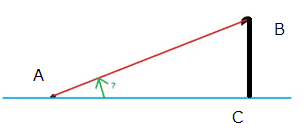
Please ignore the unnecessarily complex workaround I used to build point C in spatial tools, and the fact that I did not consider the situation when point A may not be the vertex. My two questions are:
1. In the "without spatial tools" part I extracted the coordinates as Double fields and calculate the length of AC and BC with ST_Length and CreatePoints. Then I used ArcTan(BC/AC) to determine Angle A, which turned out to be slightly different from the output from spatial tools (31.592 instead of 31.607). Could anyone tell me why and how to fix it?
(My assumption is the loss of accuracy when I try to put the coordinates in a Double field)
2. Initially I tried to calculate AC and BC by subtracting coordinates (i.e. Length of AC=Abs([X coordinate of A]-[X coordinate of B]) and naturally got the wrong results, which led me to the question: what are these coordinates used in building spatial objects? Are they longitudes and latitudes, and the positive/negative numbers tell West vs East, and North vs South? Is my assumption correct?
I have finished this but have two questions, could someone kindly provide some pointers here? Thanks!
(Please see inside spoiler)
-
Advanced
302 -
Apps
27 -
Basic
158 -
Calgary
1 -
Core
157 -
Data Analysis
185 -
Data Cleansing
5 -
Data Investigation
7 -
Data Parsing
14 -
Data Preparation
238 -
Developer
36 -
Difficult
87 -
Expert
16 -
Foundation
13 -
Interface
39 -
Intermediate
268 -
Join
211 -
Macros
62 -
Parse
141 -
Predictive
20 -
Predictive Analysis
14 -
Preparation
272 -
Reporting
55 -
Reporting and Visualization
16 -
Spatial
60 -
Spatial Analysis
52 -
Time Series
1 -
Transform
227
- « Previous
- Next »