Weekly Challenges
Solve the challenge, share your solution and summit the ranks of our Community!Also available in | Français | Português | Español | 日本語
IDEAS WANTED
Want to get involved? We're always looking for ideas and content for Weekly Challenges.
SUBMIT YOUR IDEA- Community
- :
- Community
- :
- Learn
- :
- Academy
- :
- Challenges & Quests
- :
- Weekly Challenges
- :
- Challenge #168: Dice Game - Born to Solve
Challenge #168: Dice Game - Born to Solve
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
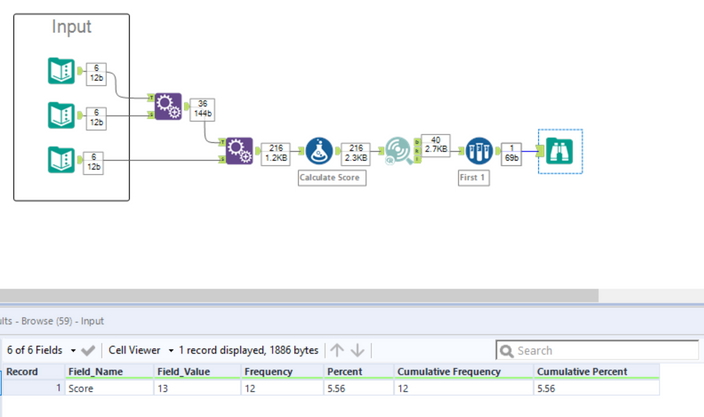
Hi @JORGE4900. I now understand your point and I had to think about this and algebraic theory of probability. Really this is two separate events: The dice roll and the math. Since each die is independent of each other, the algebraic theory of probability for any given roll is 6^3. After the roll we then apply the math rules to get our roll total. Thus, while there are 56 unique possible math combinations (thank you unique tool!), there are 216 possible rolls that need to be evaluated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Full disclosure: I attended this session at Inspire. It was fun to see my fellow weekly challengers, @estherb47 and @patrick_digan, live (and we learned how to properly pronounce @patrick_digan's name!) Since I lead a weekly challenge meetup at our office each week, I wanted to see how others articulate their thought process while solving (which @estherb47 demonstrated very well).
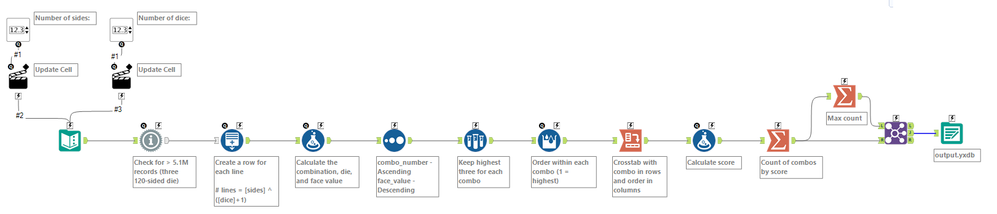
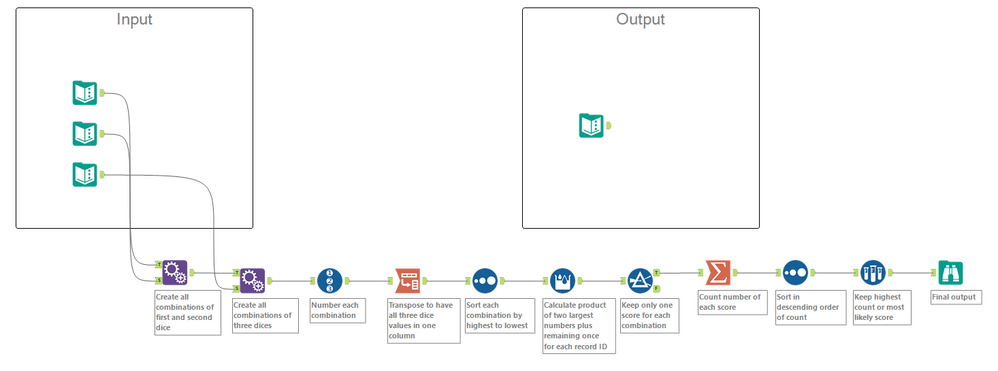
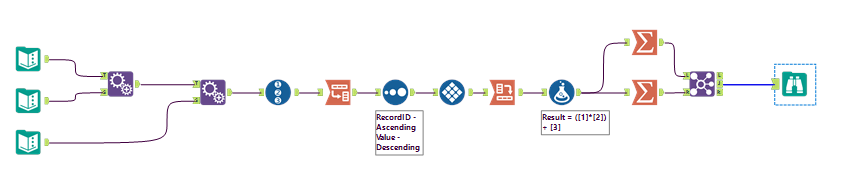
Since I'd already seen the "normal" solution, I tried to make this one dynamic (number of dice, number of sides).
As an aside, the largest number of sides available on a die is 120 ("the ultimate fair dice allowed by Mother Nature").
As another aside, with three 120-sided die, there are 136 different scores tied with a count of 183, and those scores range from 3,137 to 4,231!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Really good challenge that gets you thinking. Can't wait to review how others approached this and solved!
-
Advanced
299 -
Apps
27 -
Basic
157 -
Calgary
1 -
Core
156 -
Data Analysis
186 -
Data Cleansing
6 -
Data Investigation
7 -
Data Parsing
15 -
Data Preparation
235 -
Developer
35 -
Difficult
85 -
Expert
16 -
Foundation
13 -
Interface
39 -
Intermediate
266 -
Join
211 -
Macros
61 -
Parse
141 -
Predictive
20 -
Predictive Analysis
14 -
Preparation
272 -
Reporting
55 -
Reporting and Visualization
17 -
Spatial
60 -
Spatial Analysis
53 -
Time Series
1 -
Transform
225
- « Previous
- Next »