Have you come across a scenario where you get output different from what you were expecting for a very simple expression? Does any of the below seem familiar to you?
- Using the Fixed Decimal format with 0 to round does not work:

- Getting numbers like 2.01947e-10
- The same mathematical formula written differently returns different results:
Understanding the logic
Let us understand how the numbers work for a computer. A programming language will convert numbers into binary numbers, because computers can only understand binary numbers.
Now, it is easy to convert integers to binary, but when it comes to Decimals, it gets tricky, as not all decimals can be converted into exact binary.
1.4, for example, is represented as 1.0110011001… This is a repeating number, which means that it never ends, and 0110 keeps repeating.
Ok, so how does it matter?
Is reverse calculating this number 1.0110011001 = 1.4? No!
1.0110011001 = 1.3994140625
1.01100110011001100110 = 1.3999996185302734375
Wait… what?
This is how decimals get represented in most programming languages.
For Alteryx, 1.4 is the same as 1.3994140625, which, if rounded to 1 decimal place, will be 1.4.
Case 1
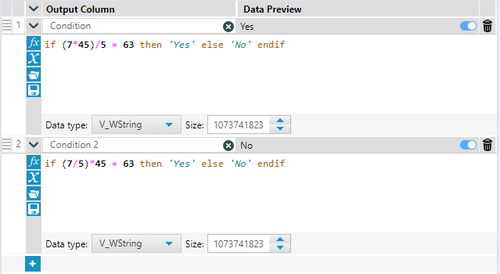
This means you will get different answers for the same expression depending on how you write it. For example, (7/5)*45 will give you the result 62.995; however, (7*45)/5 will give you 63.
This difference is taken care of if you are just doing the calculations. But if these are used inside a condition, then the differences remain, and you get different results.
This can be proven in the screenshot below.

As you can see, Expressions 1 and 2 yield the same results. However, when used in Conditions, they give different results.
To make it more interesting, let me use the expression variables in the conditions.

We got the same results as earlier. Now, what this means is that the values that we see are just visual representations, and the actual values can be different based on how we use them.
How do we use it correctly, then? We must round these values manually. Check the screenshot below.

Case 2
Let’s use Fixed Decimal to round the values.
We will start with the screenshot below.

Why is 16.5 converted to 16, while 17.5 converts to 18?
That is because the Fixed Decimal data type uses a concept called Banker Rounding. In this method, we round the middle values (like 2.5) to the nearest even number. This is a common practice in floating-point arithmetic.
Why and how is it useful?
It is done to remove any bias. For example, if we always round .5 upwards, we will get an upward bias. Let’s see an example below.
2.5, 3.5 & 4.5 total to 10.5.
- Round up: If these numbers are rounded up to 3, 4 & 5, we have a total of 12.
- Round down: If these numbers are rounded down to 2, 3 & 4, we have a total of 9.
- Banker Round: If we round these numbers to the closest even, we get 2, 4 & 4, which gives us a total of 10.
As you can see, banker rounding gives us the closest value to the actual total.
The screenshots below summarize the above concept.
Input:

Calculations:

Result:

Totals:

When should we use conversion to Fixed Decimal to round?
It is best to use it in financial data, where a large number of transactions can give large rounding differences. Hence, using Banker rounding will reduce those differences significantly.
See the example below. To demonstrate, I generated 1,000,000 rows of data.

Assign random numbers and take the sum with the Fixed Decimal conversion and then the Round function.

When we take the difference of these two with the original total, we can notice that the difference is least with Fixed Decimal.
When do we use the Round function? We will use Round in cases such as Case1 above.
Case 3
In some cases, you would have seen numbers like 2.00001e-2, etc. Now these are called scientific numbers.
The number 2.00001e-2 is just 0.0200001. But what is confusing is why this number even exists. I just added two simple numbers; why did it give us a scientific number?
The answer is again binary conversion. See below.

As you can see from the screenshot above, I have two very basic numbers, 24.4 and -24.2. In the Summarize tool, I am going to sum up these two numbers. Logically, the answer should be 0.2 as shown in the screenshot below. But what is that red arrow?

If we dig deeper, we will see that the output is something else, see below.

Interesting, isn’t it?
This is again because 0.2 does not have exact binary, so it is represented as repeating binary numbers 0.0011… with 0011 repeating.
So, 0.2 = 0.1999999999, though not mathematically.
Conclusion
I hope that now you understand how numbers work differently in Designer, and how you can create better solutions.
Here is some guidance when working with these scenarios:
- Use Fixed Decimal to reduce the rounding differences in totals.
- Be careful with calculations when used inside conditions.
- Don’t turn your eyes away from those small red corners in the result pane.
Remember, everything boils down to Binary!














