Data Science
Machine learning & data science for beginners and experts alike.- Community
- :
- Community
- :
- Learn
- :
- Blogs
- :
- Data Science
- :
- Introducing the Alteryx Simulation Toolset
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
The recent 10.6 Predictive Release includes the introduction of the Prescriptive Category (Optimization and Simulation). This blog post will demonstrate some different uses of the 3 new simulation tools (Simulation Sampling, Simulation Scoring, Simulation Summary) via an example use case. Alteryx 11 now contains this sample workflow in the help section in the Prescriptive Analytics category.
THE PROBLEM
Imagine you're a company selling hard drives. You've sold some in the past with 2-year, 3-year, and 4-year warranties and are wondering which warranty length would maximize your profit on your new $139.99, 7200RPM, 2TB HDD. You already have some data from past sales:
- Percent of hard drives that were DOA (5.8%)
- Dataset of non-DOA hard drives sales with their IDs, whether they failed in the first 5 years, and their failure months
- Linear Regression model giving demand (number of sales) as a function of price, warranty (for 2/3/4 as dummy variables), RPM (5400 or 7200 as dummy variables), and hard drive size.
It makes sense to sort this into a few components:
- Create sample of HDDs noting whether they failed and in which month
- Take scores of the model against $139.99, 7200RPM, 2TB HDDs at 2, 3, and 4 year warranties.
- Combining both into a profit function
HDD SAMPLES
First, we need to decide how many samples to make. 100,000 samples with 5.8% DOA and a similar number dying between 0 and 5 years should be an adequate amount to model on. Now, we can simulate the number of DOAs via a Simulation Sampling tool:
Since this is our first part of the simulation, we don't connect anything to the S(imulation) input:
For sampling mechanism, we select Monte Carlo Sampling. Latin Hypercube Sampling would also be a fine choice. Monte Carlo is more random, Latin Hypercube is faster converging.
For chunk size, 100,000 records should fit easily into memory, so anything larger than 100,000 is appropriate.
We choose any random seed. This is done so that results will be repeatable. Select the same seed as above (1) to replicate the sample results.
We decided 100,000 was a good size for the sample.
We only have a parameter (.058 = 5.8% of HDDs are DOA), so we will choose to sample parametrically. For parametric sampling, we don't connect anything to the D(data) input because we're sampling based on parameters, not Data.
Clicking Next will bring us the parametric sampling tab:
We are modeling DOA units, so that is an appropriate name for the field that will be output.
Having 5.8% 1s (DOA) and 94.2% 0s (non-DOA) can be modeled with a Binomial distribution with 1 Trial and a probability of .058.
The Bounds should just include the range [0,1] since we want all of the results (and we can see from the graph that all of the results return 0 or 1).
The output DOA column will then just be a column of 0s and 1s:
We have a dataset on failures of non-DOA HDDs, but we want to combine it with the data we just generated to get a look at the big picture. Filtering on the DOA column lets us look at the non-DOA HDDs and simulate on that. We also notice that there's a seed field with our previous seed value incremented.
We connect the data we wish to sample to the D input and the simulated data to the S input.
Upon doing this, we immediately notice some differences; there is no choice for the seed or for the number of iterations. This is because when data is connected to the S input, the number of iterations is determined by the number of records in that dataset, and if a seed field is present in that data, that seed is used automatically. Since we have data to sample from, we select sample from data and proceed.
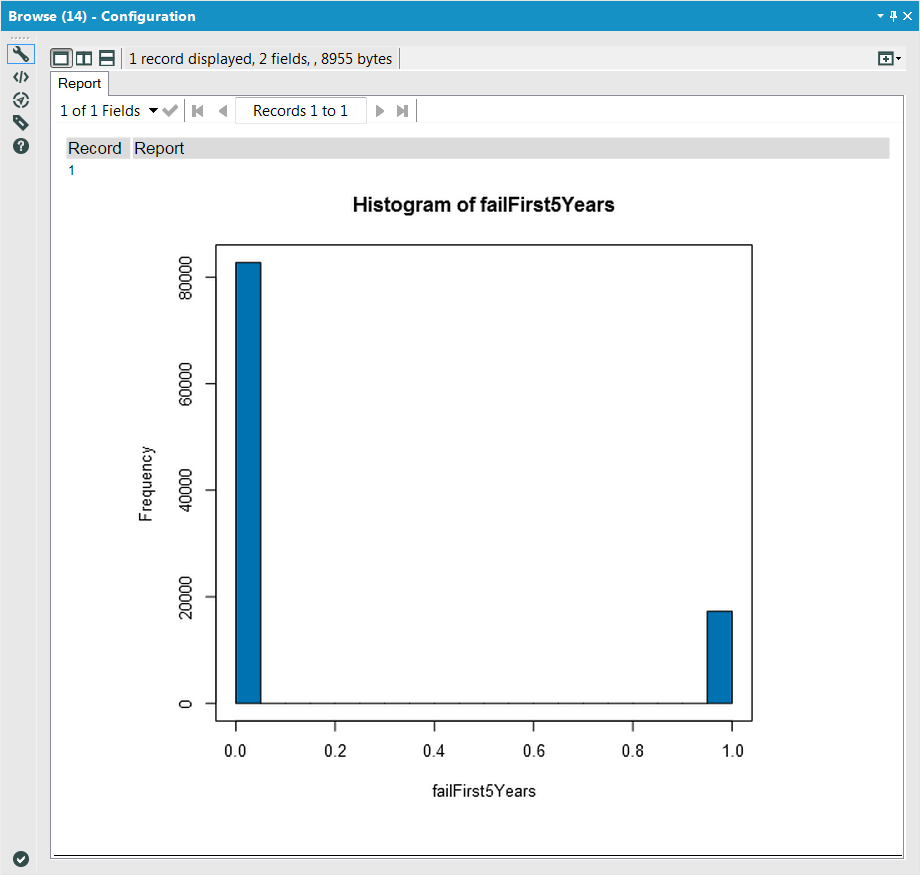
Here, we are looking to fit (i.e. fit to a distribution) the binary indicator (0/1) column failFirst5Years to a Binomial Distribution to get a distribution of the ones that fail in the first 5 years after arriving, so we select those in the appropriate components of the configuration. Since we have data which is not binned, we also select the raw data option.
Similarly to the DOA instance, we will get an output column of 0/1s for the failFirst5Years variable as well as the seed, but this time (since we connected the S Input), it will also include previous data (ID, DOA) appended:
Lastly, we need to get the failMonth for all HDDs that failed in the first 5 years. We can do this by going back to the dataset we have, getting only the failures, and sampling failMonth from there:
The connections and first phase of the configuration should look familiar from before.
Here, instead of fitting the data to a distribution, we want to sample directly from the data. There are two options here: sample entire rows and sample each column independently. These both sample from data, but the former preserves items along the same row. In the case of only sampling from 1 column, they are identical. We choose here to not Sample with replacement, but that option can be chosen and must be chosen when the D has fewer records than S.
The output format is what we'd expect, incrementing the seed and appending the samples of failMonth to the previous data:
Unioning the DOA and non-DOA (FailMonth) data back together, we can get an idea of how we'd expect the failures to build up over time (of the original 100,000):
and unioning in the non-failures gives us ideas of the number of failures / non-failures of our 100,000 sample size:
Demand Model
The second component will use the Simulation Scoring Tool to get an idea of the distribution of possible warranties for each warranty option. First, we need to get the data in an appropriate form for our linear model object:
This must contain every field (with the same names and types) that the model was trained on.
Since our model object was created by a linear regression tool, we do not need to connect a dataset to the V(alidation) input; for all other model objects, connecting a Validation input is necessary. We connect our model to the M(odel) input and our data to score (the table above) to the S input:
Similarly to the Score Tool, we select our output field name, and similarly to the Simulation Sampling Tool, we select the chunk size and random seed. Here, though, we also have the option samples from error distribution. The Simulation Scoring Tool allows us to make draws out of the error distribution of the model object when scoring. This number is the number of draws to make from that error distribution. If we look closely, we'll notice each collection of 3 records repeats (and the same as the stream going into the S input) except for our score output field in the output data:
If we do a little manipulation and filtering (converting the dummy variarbles back into warranty numbers), we can look at the expected number of sales for a 2 year warranty:
3 year warranty
and 4 year warranty
OPTIMAL WARRANTY DURATION
Now that we have distributions for the expected sales for each warranty duration and the expected lifetime of a HDD, we can implement a profit function (see more in Formula Tool 57 of the linked example) and see which is the optimal choice to maximize profit:
We can use the Field Summary Tool to view a distribution and summary stats for each warranty length. It would seem that a 4 year warranty is optimal. We can use the Simulation Summary Tool to verify this:
Selecting warranty as an input variable and profit as an output variable includes a plot of the two against each other in the R(eport) output:
In both, we see that the 4 year warranty seems slightly better for profit than the 3 year warranty and much better than the 2 year warranty and also has less variation in expected profit.
IN CONCLUSION
We've seen in the above example that the new Simulation Toolset can be used to model uncertainty (DOAs, other failures, demand) as well as to get an idea of the distribution around an expected value. If we wanted to go a step further, it would make sense to vary the price and see what our optimal price/warranty combination is for maximizing profit.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.