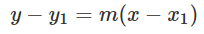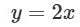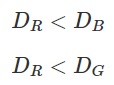Data Science
Machine learning & data science for beginners and experts alike.- Community
- :
- Community
- :
- Learn
- :
- Blogs
- :
- Data Science
- :
- What is Linear Regression? A Qualitative Explorati...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
When it comes to statistical modeling few things are as tried and tested as linear regression. It's simple, it's (fairly) easy to conceptualize, and fast. Unfortunately, most of the articles I've read about it feel closer to math textbooks than to layman's definitions. In this post I'll give a fairly informal definition of linear regression, overview the goals of linear regression, and talk about a few things you can use it for.
Caveat lector: this post intentionally avoids rigorous mathematical definitions of linear regressions!
Try Googling It
In statistics, linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple linear regression.
Google Results for what is linear regression
Oh, well now it's all so obvious :). There are some scary words in there: scalar, dependent variable, explanatory variable, and even this thing called simple linear regression. What-the-what? I thought I was already looking for the simplest definition!
But have no fear. I'll explain all this to you without using too much math.
Close up of the maths
A Brief History Lesson
This all started in the 1800s with a guy named Francis Galton. Galton was studying the relationship between parents and their children. In particular, he investigated the relationship between the heights of fathers and their sons.
Mr. Galton
What he discovered (as you might expect) was that a man's son tended to be roughly as tall as his father. However Galton's breakthrough was that the son's height tended to be closer to the overall average height of all people.
Let's take Shaquille O'Neal as an example. Shaq is really tall, 7 ft 1 in to be exact (for you metric fans that's about 2.2 meters). If Shaq has a son, chances are he'll be pretty tall too. However, Shaq is such an anomaly that there is also a very good chance that his son will be not be as tall as he Shaq.
Mr. O'Neal
Turns out this is the case: Shaq's son is pretty tall (6 ft 7 in), but not nearly as tall as his dad.
Galton called this phenomenon regression, as in "A father's son's height tends to regress (or drift towards) the mean (average) height."
If you're interested in Galton's work, you can see his wonderfully titled essay, "Regression Towards Mediocrity in Hereditary Stature" here.
A Simple Example
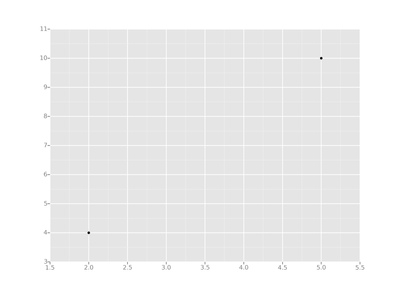
Let's take the simplest possible example: calculating a regression with only 2 data points. Now while the statistician in the room might be quaking in fear at the thought of this, I think it'll help get my point across :).
All we're trying to do when we calculate our regression line is draw a line that's as close to every dot as possible. For classic linear regression, or "Least Squares Method", you only measure the closeness in the "up and down" direction (there are plenty of other ways to do this, but to be honest it usually doesn't matter).
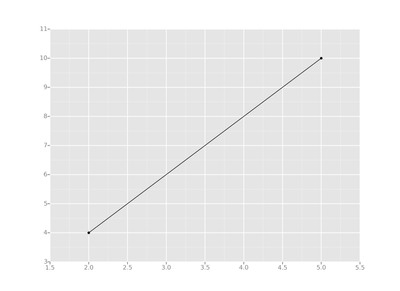
So if you draw a straight line that is as close as possible to each of our 2 points, you get something like this:
This is great! Our line crosses through both data points (this is also the definition of a line). If we want to calculate the equation of this line, we can use the slope formula:
Plugging in our of our points we calculate our line to be:
Now hopefully you aren't too impressed by this, but this is in some sense the basis of what a linear regression is!
Scaling Up from There
Now wouldn't it be great if we could apply this same concept to a graph with more than just two data points? By doing this, we could take multiple men and their son's heights and do things like tell a man how tall we expect his son to be...before he even has a son!
Below, we see 1000 father/son height combos.
To roughly estimate a regression line, it's pretty simple: Just draw a line that is as close as possible to every point on your graph. Now this might be a little tedious to do by hand, but you'd be surprised at how close you can come just by eyeballing things.
A Little More Complex
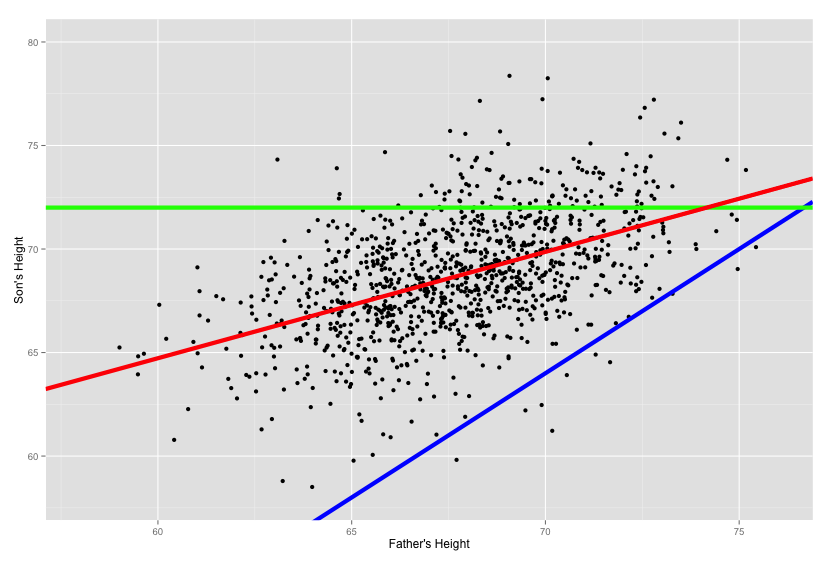
We can use the same approach we used with 2 points, but now that we have 1,000 data points this is a bit more complex. Below is the result of the linear regression, with the fitted line in red.
I've used R to create the regression, but there are tons of ways to do this (see below).
A critical question to ask at this point is why this line? Why not a line with greater slope or even more extreme, a vertical line? Furthermore, how can we claim that this line is the best and what is it mean to be the best line?
Let's compare the red line to two other other lines below:
Clearly these two lines don't fit our data very well. But what does that mean mathematically?
Without getting in too deep into the math, if we refer back to earlier in the post, we mentioned that our goal with linear regression is to minimize the vertical distance between all the data points and our line. So in determining the best line, we are attempting to minimize the distance between all the points and their distance to our line. There are lots of different ways to minimize this, (sum of squared errors, sum of absolute errors, etc), but all these methods have a general goal of minimizing this distance.
In our example, we can see that if we were to take the total vertical distance between the points the the red line DR, and the total vertical distance between the points and the green DG or blue line DB, the total distance between the points and the red line is smaller.
In pseudo-mathematical terms:
There are more robust mathematical proofs to show this, but we won't get into that here. If you're interested in reading more about this, I recommend Khan Academy's Tutorial.
What next?
Linear regression is a powerful tool that you can do some really cool stuff with.
From just this example you could estimate how tall a man's son will be before he has one, determine which of your friends is freakishly tall with respect to their dad, or even compare different groups of men and their sons over time to analyze trends.
One day, Simba, you will be 4' 10".
While this post intentionally breezes over the math aspects of linear regression, its undeniable that to use linear regression in practice, you need to have a thorough understanding of both the qualitative and quantitative characteristics of the regression. As the number of inputs to a model increases, so does its complexity and it is important to understand the ramifications of this to be able to make sense of your model. This is nearly impossible to do without understanding the math behind these statistical techniques. That said, linear regression is a great place to start learning statistical modeling techniques, and the links below should help you get going!
Other Resources
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.