Data Science
Machine learning & data science for beginners and experts alike.
It can feel overwhelming to get started with the Predictive tools in Alteryx, especially if you are brand new to predictive modeling in general. For this article, we were fortunate enough to exploit the knowledge of our favorite econometrician @HossC, but he may not be available in your time zone. Have no fear! The trick to successfully getting started is understanding your data, then understanding the tools and models that match your data.
This post will help you get up and running by discussing the different types of variables you might want to estimate with a predictive model, as well as which algorithms are available to you in Alteryx Designer for each data type.
It is important to remember that predictive modeling is an iterative process that involves testing, more testing, and comparing the results from multiple models. There will almost always be more than one predictive algorithm (and corresponding tool) that is appropriate to use with your data. There is no reason to prefer one algorithm over another without first looking at and experimenting with your data.
As another PSA, we’d like to remind you to always start your predictive journey with data investigation. For help getting started with data investigation in Designer, check out our Pre-Predictive series: Pre-Predictive 1, Pre-Predictive 2, Pre-Predictive 3, and Pre-Predictive 4. Once you feel good about the state of your data, you can start experimenting with algorithms!
Choosing Your Algorithm
The biggest determinant of appropriate algorithms and methods to use with a dataset is the target variable. The target variable (also known as the dependent variable) is what you are trying to predict, whereas a predictor variable (independent variable) is what you think will impact the values of the target variable. Here, we will cover four types of target variables:
Qualitative (Categorical) – non-numerical
- Binary - strictly 2 possible values (e.g.: true/false)
- Multinomial - more than 2 values
Quantitative (Numeric)
- Continuous - can take any numerical value and are measured
- Count - variables are numeric, non-negative, and result from counting rather than ranking
1. Qualitative: Binary
A variable with only two possible categorical values are called binary variables. Common examples of values in a binary field are Yes and No, 1 and 0, etc.
For the R tool to handle it properly, a binary variable needs to be set as a non-numeric (preferably string) data type. If the data type is left as numeric, then models will interpret the target variable as a continuous variable (see below). Your target field should only contain two discrete values, 1 and 0, which is why we want to ensure the variable is non-numeric.
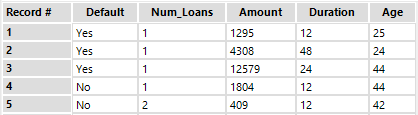
For example, let’s look at a snippet of data about loans:
The target variable in this example is [Default], as we’re trying to answer the question “Did the borrower default on their loan?” Since the two possible outcomes of this question are Yes or No, we know that our target variable is binary.
In general, the target variable should have a fairly uniform distribution; in the binary case, as close to a 50/50 split as possible. If the variable is skewed to either side, it will be harder for the model to evaluate the other predictor variables. If your distribution is uneven, consider oversampling your data.
The predictions of a binary target variable will result in the probability of that result occurring. If not pre-selected, algorithms usually default to the positive class (the class that is deemed the value of choice; in a Yes or No scenario, it is most commonly Yes. It is important to remember that the question is never, “will X happen?” it is “how likely will X happen?”
The following algorithms work with a binary dependent variable: Logistic Regression, Boosted Model, Decision Tree, Forest Model, Naïve Bayes Classifier, and Neural Network
2. Qualitative: Multinomial
Multinomial variables are categorical variables that have 3 or more values.
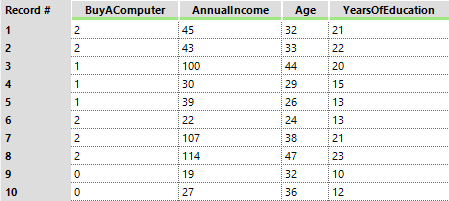
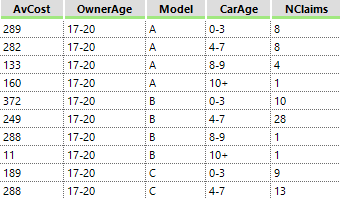
In the following example, we are trying to predict how likely a consumer is to buy a computer this year. The target variable [BuyAComputer] has three possible values: 0 = Not Very Likely, 1 = Somewhat Likely, 2 = Very Likely
In the same way that binary models give probabilities for the positive (Yes) and the negative (No), multinomial models will give probabilities for each value fed into the model. Similarly, the question is never “which option will happen?” it is “how likely will option X happen?”
Like binary models, your multinomial target should also have a fairly uniform distribution. Since the number of values can vary, the split will always depend on the number of values. In the [BuyAComputer] scenario, the number of values is 3, so the split should as close to 33/33/33 as possible.
The following tools support qualitative multinomial dependent variables: Decision Tree, Forest Model, Boosted Model, Neural Network, and Naïve Bayes Classifier
3. Quantitative: Count
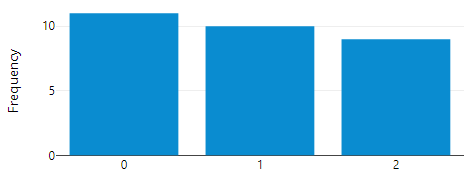
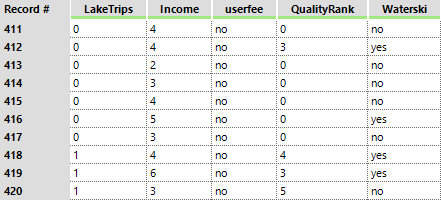
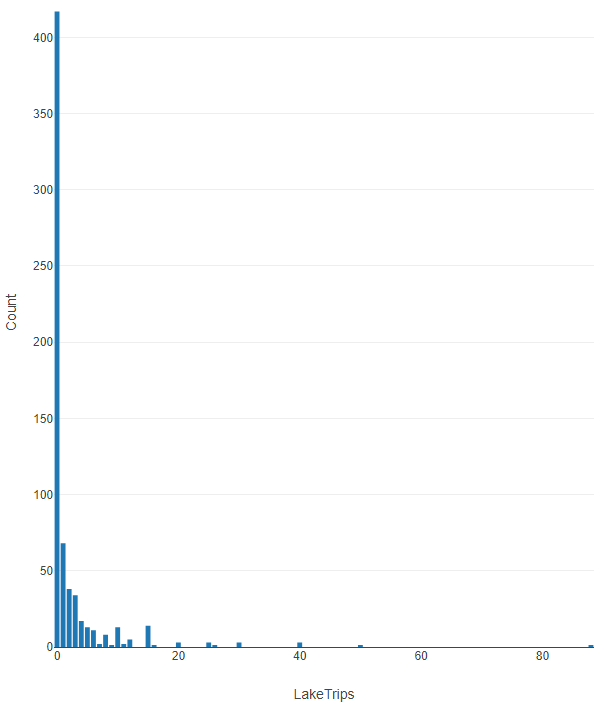
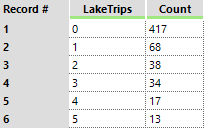
Count variables are numeric non-negative integer values {0, 1, 2, 3, ...} that represent the number of times an event occurred. These variables are not continuous, as the values cannot be logically sub-divided into smaller increments. Count variables have a very distinct distribution of values, where the most occurring value is 0, then the second highest will be 1, and then 2 and so on. If it does not follow this pattern, then it is not considered count data. Consider the example below, predicting how many lake trips will be taken (target = [LakeTrips]):
The frequency of the [LakeTrips] variable is seen below, which qualifies as count data:
The tools that support quantitative count dependent variables: Count Regression, Spline Model, Decision Tree, Forest Model, Boosted Model, and Neural Network.
4. Quantitative: Continuous
Continuous variables can be subdivided into as many decimal places as needed, making the possible values numerically continuous, i.e. infinite.
It is important to note that predictions with continuous variables can result in negative numbers and irrational numbers (numbers with never-ending decimals). Even if the right algorithm is selected, it is still vital to understand the limitations that go with your use case.
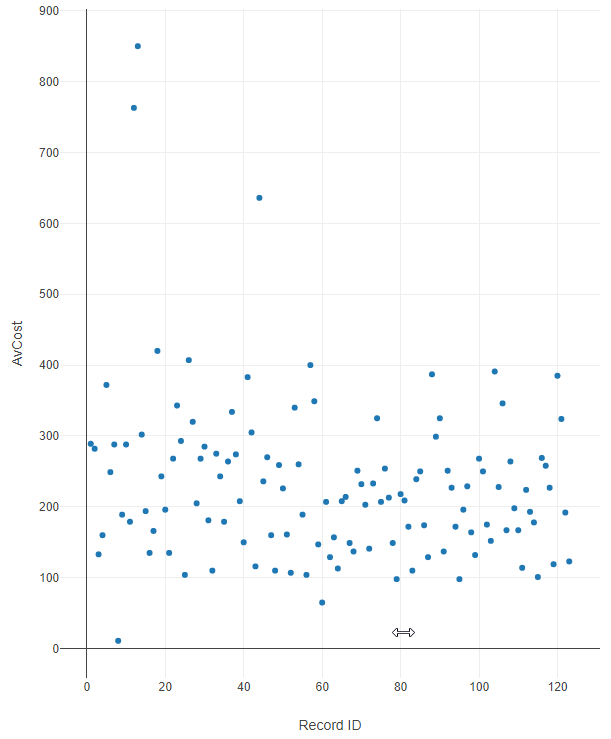
An example of a continuous target variable is average cost. The predicted average cost ([AvCost]) of a car insurance claim can be any amount of dollars and cents.
Since the split of the data can be a range of decimals and values, the most appropriate representation of these data would be a Scatter Plot, where each value, more or less, is unique to the target variable.
The tools to use with quantitative continuous dependent variables are Linear Regression, Gamma Regression, Boosted Model, Spline Model, Decision Tree, Neural Network, and Forest Model.
Cheat Sheet
Who doesn’t love a good cheat sheet! Below is a diagram that can be used as a reference guide for when you are choosing your algorithm and have identified your target variable.
Additionally, attached is a workflow that provides simple examples of each model that works with each type of predictor variable. Feel free to check it out and explore how your data fits into each model.
Now that you have defined the type of dependent variable you will be using, you are ready for data investigation, data preparation, and data modeling. Remember to fully understand your use case and data, and check if the output makes sense to you. Predictive Modeling is an iterative process and it takes time to create that best model.
Thanks again to Hoss Carroll for his help with content, the attached mind map, and sample workflow. Happy Alteryx-ing!
