Alteryx Designer Desktop Discussions
Find answers, ask questions, and share expertise about Alteryx Designer Desktop and Intelligence Suite.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- Designer Desktop
- :
- Re: What is the easiest way to cut off a segment o...
What is the easiest way to cut off a segment of a circle?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
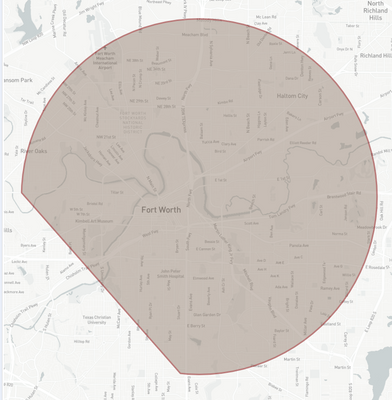
I have a problem in that I have a circle and a triangle as defined by my data such that the triangle is made up of the centre of the circle and two points on the circumference as shown below:
So, if I overlay the shapes as shown above it forms 3 distinct areas the main part of the circle shaded pink, the triangle shaded white (or not shaded might be more accurate), and then the smaller segment of the circle that I have shaded yellow. What I am looking to have as a result is the area of the circle minus the yellow segment which means that it will consist of the pink and white areas.
Is this possible without resorting to advanced maths and creating arcs etc.... I am not confident enough with the spatial processing tool's capabilities to not dismiss that there is just this functionality hiding somewhere within the capabilities of Alteryx. Or perhaps as part of the Formula functionality.
Any help or pointers gratefully received.
Peter
Solved! Go to Solution.
- Labels:
-
Spatial Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you provide sample data? If the shapes are in there as spatial objects you can use a Spatial Info tool to find the areas. Otherwise, it depends on the data you have.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well this is a fun spatial problem, and a great application to learn about the Spatial Process tool!
https://help.alteryx.com/20221/designer/spatial-process-tool
In the attached workflow, I start by creating two polygons: the circle and the triangle (which I believe is your starting set of data). The Spatial Process tool can be used to cut the triangle section from the circle, leaving two polygons, the pink and yellow sections in your image. I use the area of the two polygons to determine the smaller (yellow) area and sample my records to only that polygon. Now that we have the yellow area, we can use the Spatial Process tool again to cut the yellow section from the original circle, leaving what would be the pink+white areas of your above image. I believe this is what you were looking for.
Now this may not always work as there are several conditions that must be met regarding how the triangle is defined (if you have points or a polygon) and if the radius points lie exactly on the circle perimeter or not. It should also be possible to Spatial Process to merge the pink and white areas. We can discuss further for any of these cases, but this should help get the conversation started!
PS: The workflow has browses in important places that I recommend viewing to follow along what's happening.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Just wanted to write a quick thanks for solving my issue. I am not completely sure why you seem to have some duplicate steps in the workflow, but I am working my way through it and trying to understand why as it is very effective.
Many thanks again,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Happy to help! Is there something in the workflow that I can help clarify? The container names should describe what each section is doing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
No, it's just that my points aren't exact, so the two other points do not lie on the circle's circumference which is causing some problems as you predicted.
The radius is 5.75389725 miles.
Point Lat Long
No 1 53.39194 0.23167
No 2 53.49222 0.08417
Centre 53.47500 0.22083
But thanks again,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah yes, that would cause an issue. I took another crack at it and came up with some ideas about how to work with that situation.
I started by building a circular polygon. This could be done by using the defined value you provided (5.75389725 miles), or the average distance of the two points if you want to use them as much as possible. This polygon is then converted to a ring/line using the ST_Boundary( function in the Formula tool and use the Distance tool function "Create the nearest point" checkbox to create a point along the ring nearest the original points. Now we have points along the circle which we can use to build the triangle object from.
Once we have the circle and triangle polygons built, I used the same process from the first workflow to create the desired object.
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
What a great solution and very inventive thinking....
Still looking through it but was very clear and very well worked out.
Many, many thanks again,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
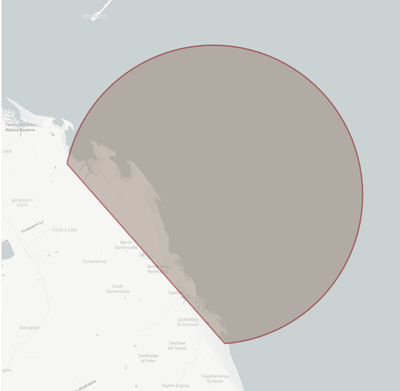
Hope that are not too bored yet but found an edge case of a straight line across the circle which seems to 'break' the solution.
The points are:
No 1 51.63750 -4.73000
No 2 51.63750 -4.83667
Centre 51.63750 -4.78333
Thoughts welcomed....
Kind regards,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
PS - I am looking for the southern half as the desired output...
-
Academy
6 -
ADAPT
2 -
Adobe
203 -
Advent of Code
3 -
Alias Manager
77 -
Alteryx Copilot
24 -
Alteryx Designer
7 -
Alteryx Editions
91 -
Alteryx Practice
20 -
Amazon S3
149 -
AMP Engine
250 -
Announcement
1 -
API
1,207 -
App Builder
116 -
Apps
1,359 -
Assets | Wealth Management
1 -
Basic Creator
14 -
Batch Macro
1,554 -
Behavior Analysis
245 -
Best Practices
2,691 -
Bug
719 -
Bugs & Issues
1 -
Calgary
67 -
CASS
53 -
Chained App
267 -
Common Use Cases
3,820 -
Community
26 -
Computer Vision
85 -
Connectors
1,425 -
Conversation Starter
3 -
COVID-19
1 -
Custom Formula Function
1 -
Custom Tools
1,935 -
Data
1 -
Data Challenge
10 -
Data Investigation
3,485 -
Data Science
3 -
Database Connection
2,217 -
Datasets
5,216 -
Date Time
3,226 -
Demographic Analysis
186 -
Designer Cloud
739 -
Developer
4,364 -
Developer Tools
3,525 -
Documentation
526 -
Download
1,036 -
Dynamic Processing
2,935 -
Email
927 -
Engine
145 -
Enterprise (Edition)
1 -
Error Message
2,253 -
Events
197 -
Expression
1,867 -
Financial Services
1 -
Full Creator
2 -
Fun
2 -
Fuzzy Match
711 -
Gallery
666 -
GenAI Tools
3 -
General
2 -
Google Analytics
155 -
Help
4,704 -
In Database
965 -
Input
4,290 -
Installation
360 -
Interface Tools
1,900 -
Iterative Macro
1,091 -
Join
1,956 -
Licensing
252 -
Location Optimizer
60 -
Machine Learning
259 -
Macros
2,858 -
Marketo
12 -
Marketplace
23 -
MongoDB
82 -
Off-Topic
5 -
Optimization
750 -
Output
5,246 -
Parse
2,325 -
Power BI
227 -
Predictive Analysis
936 -
Preparation
5,161 -
Prescriptive Analytics
205 -
Professional (Edition)
4 -
Publish
257 -
Python
853 -
Qlik
39 -
Question
1 -
Questions
2 -
R Tool
476 -
Regex
2,339 -
Reporting
2,429 -
Resource
1 -
Run Command
573 -
Salesforce
276 -
Scheduler
410 -
Search Feedback
3 -
Server
628 -
Settings
933 -
Setup & Configuration
3 -
Sharepoint
624 -
Spatial Analysis
599 -
Starter (Edition)
1 -
Tableau
512 -
Tax & Audit
1 -
Text Mining
468 -
Thursday Thought
4 -
Time Series
430 -
Tips and Tricks
4,184 -
Topic of Interest
1,126 -
Transformation
3,721 -
Twitter
23 -
Udacity
84 -
Updates
1 -
Viewer
3 -
Workflow
9,965
- « Previous
- Next »
![20221129 - PV - Shape Cut Out].png 20221129 - PV - Shape Cut Out].png](https://community.alteryx.com/t5/image/serverpage/image-id/271539iB1D77EBD643CC1C3/image-size/medium?v=v2&px=400)