Comparison table

[CainR]

Hi Team

Currently I want to be able to do a table that has the same Rows and Headers, the ouput that is desired would look like this

	Bob	Derek	Jennifer	Sally
Bob	x	Std Dev	Std Dev	Std Dev
Derek	Std Dev	x	Std Dev	Std Dev
Jennifer	Std Dev	Std Dev	x	Std Dev
Sally	Std Dev	Std Dev	Std Dev	x

Column Bob Row Derek would ideally show the standard deviation of those two names records. 

The data that I have as a rough example looks like this.

Name	Values
Bob	5
Bob	6
Bob	5
Bob	7
Bob	9
Derek	12
Derek	10
Derek	8
Jennifer	7
Jennifer	7
Jennifer	7
Jennifer	5
Jennifer	8
Sally	20
Sally	18
Sally	21

Could someone please offer some assistance in figuring this out?

Thanks

[KaneG]

Hi @CainR,

In order to do this, you would need to calculate the StdDev for each combination and so working backwards, you want to get to a table that has the following Columns:

• [Name]
• [Name2]
• [StdDev]

so that you can eventually crosstab that in to your required format.

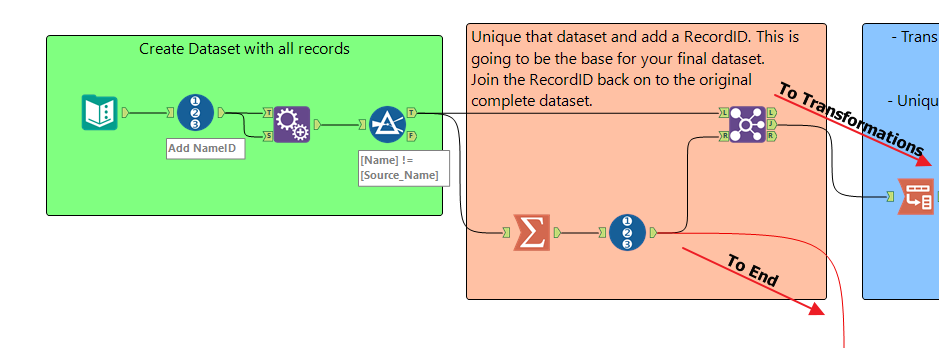
To Do that, you would append the dataset to itself and then remove the records where Name==Name2 (Note, this would be bad if the dataset had > 1000 records, in that case, you would employ a slightly different method). 

After that, you can make a Unique set of combinations as a base for your final dataset before grouping all the records in such a way that you can summarise to work out the StdDev and then Join that back on to the clean dataset.

I've attached a module to do this, however there may be an easier way if your dataset is more defined or the reasson is more defined.

Kane

[CainR]

Hi Kane

Thanks for the help and quick response, the purpose of this is to do a comparison of averages, std deviations and coefficient of variation across all the possible combinations in the matrix, there will be a seperate matrix for each value. This highlights to my team areas of potential interest. The current workflow is great for the small scale however I should have specified that the dataset has >1000 records. Could you please demonstrate the alternative method you mentioned?

Cheers

[Joe_Mako · Accepted solution]

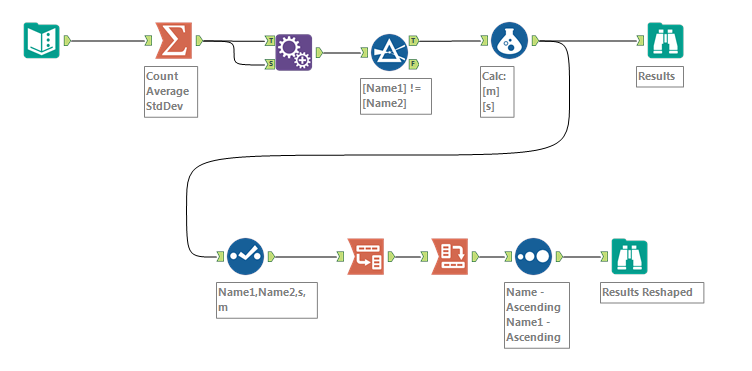
Here is a route that takes advantage of combining the aggregations. The attached computes aggregrations to the Name granurality, appends to get all potential name pairs, then computes the combined average and standard deviation. I also added some steps to reshape the results into the output you requested.

For Combining Standard Deviations and Averages, see:
http://stats.stackexchange.com/questions/55999/is-it-possible-to-find-the-combined-standard-deviatio...

in the code below:
m=Average
n=Count
s=Standard Deviation

m=
(m1*n1+m2*n2)/(n1+n2)

s=
SQRT(((n1-1)*POW(s1,2)+(n2-1)*POW(s2,2)+n1*POW((m1-m),2)+n2*POW((m2-m),2))/(n1+n2-1))

For Combining Correlation Coefficients (did not do in the attached), see:
http://mathoverflow.net/questions/57908/combining-correlation-coefficients

This should work fine if you have a few thousand names (but the crosstab would be insane), and if you want to be even more efficient, just calculate one side of the diagonal by changing the filter from:

[Name1] != [Name2]

to

[Name1] > [Name2]

[KaneG]

Well, there you go... the example from @Joe_Mako is pretty on the money.

I didn't have a solution in mind when I referred to a slightly different method as I just quickly built out what first came to mind, but more aggregation/processing would have to be moved to before the append and that's what Joe's solution does. I like that solution because it offers the best reduction of processing speed.

However if you wanted to do it without the formula tool, I've attached a version that does that as well as I wanted to see if my brain was on the right track as to what I thought could be done.

Kane