Maveryx Success Stories
Learn how Alteryx customers transform their organizations using data and analytics.STORIES WANTED
Showcase your achievements in the Maveryx Community by submitting a Success Story now!
SUBMISSION INSTRUCTIONSPrescriptive Analytics: Unleash the Optimization Tool
Overview of Use Case
Philip Mannering started using Alteryx two years ago. During that time, he became Alteryx Designer Expert Certified and won the Grand Prix at Inspire Nashville. Philip shares his expertise in this use case and demonstrates how to solve a problem with one or two variables. He goes further to explain how prescriptive analytics and the Optimization Tool can help you find the best solution to your most pressing questions.
There are three types of analytics: descriptive, predictive, and prescriptive. In that order is often how businesses first try to use data. They might start with the basic descriptive and then go to predictive and then quite possibly prescriptive after that. It's generally regarded that goes from easier to harder and you might get more value if you make it to the far.
Descriptive analysis shows what happened, predictive is what will happen and prescriptive tells you exactly what you should do. So prescriptive will give you the best answer, it tells you exactly what you should do, and it's not based on predictions that are stochastic or based on probability. It's saying literally "this is what you should do." Optimization goes by a few names, one is "linear programming" and "operational research" is another term for it. But essentially, all those things boil down to two things. You need an objective function, that's the thing that you want to optimize, either maximize of minimize, and a set of linear constraints.
Solving for one decision variable
A trivial example to show how to formulate the problem and start using the Optimization tool.
Question: How many Hershey Bars, 𝒙 should I make to maximize profit if each bar costs £0.9 and I’m constrained by amount of ingredients?
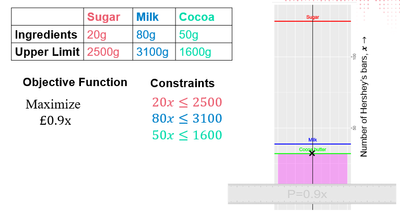
The goal is to choose an "x" for the number of chocolate bars that you need to make to maximize the profit if each costs 90p. There is only one decision variable and that's how many bars of chocolate. If you just plot the constraints on one axis you can see that cocoa butter is the limiting constraint. Milk and sugar are just redundant constraints in this case. And so, at the graph above you can find the optimum answer. So, if you were to put this into the Optimization tool this is how it would look:
You have the objective function and the variables "coefficient" and "type I”, that "I" stands for "integer". Then you got the constraints. So, 20x has to be less than or equal to 2,500, 80x has to be less than or equal to 3,100, etc. And then the output, this isn't an arbitrary objective value, this is the total profit. So, it’s saying you can make 32 bars of chocolate "x", 32x is 32, that's the number of bars of chocolate you make. And if you times that by .9 you get 28.8. So that's the profit.
Solving for two decision variables
Let’s up the stakes and see how the workflow is set up for two variables. We introduce tool configuration “variables in rows” to support the structure of the input data.
Question: How many bars of Hershey’s, 𝒙 (£0.9) and Hershey’s Cookies and Crème, 𝒚 (£1.0) should I make to maximize profit?
So now you have two bars of chocolate, Hershey's and cookies and cream. Now the objective function is to optimize 90% times X- and one-pound times Y. And of course, the more decision variables you have, the longer this series becomes. You still have the same constraints, but now you have two decision variables, the Hershey bar in X and number of cookies and cream bar in Y. In the graph below we plotted these constraints to find the profit. If we chose any single profits, this is the line it would make: 0.9x plus 1y. Everything in this magenta region is a feasible region. So, that's within the constraints. The optimum solution is 10 Hershey bars and maybe 46 cookies and cream bars. The total profit is 55. That was more than the profit when we just made the single chocolate bar before. So, if you were to put this into the Optimization tool this is how it would look:
To take your analysis to the next level in your business:
- Identify a business problem that requires optimizing
- Set the Objective Function (the thing you want to optimize)
- Set the List of Constraints (the things limiting you)
- Prepare you Inputs (correct structure, column names, data types, etc)
- Interpret and present your results
Ever wonder what activities you could do in London with a time constraint? How about how to maximize the value of your fantasy football team on a budget? Or want to learn more about why to change the option from constraints in rows to variables in rows? The entire PowerPoint presentation can be found here.
