チャレンジ #266: N乗と、その先へ

[AYXAcademy]

こんにちは、Maveryx！

先週のチャレンジの回答はこちらで見つけることができます。

今週のチャレンジは、Patrick Digan (@patrick_digan)によって提供されました。Patrick DiganはACEであり、コミュニティ活動にも積極的で、これまで数多くのウィークリーチャレンジを提供してくれています。Patrickさん、ありがとうございます！

今週のチャレンジは、つい先日に過ぎ去った、とある特別な日・・・そう円周率の日にちなんだ問題です！美味しいご馳走ではなく、無限に続く繰り返しのない小数：3.14…が3月14日に祝われます。

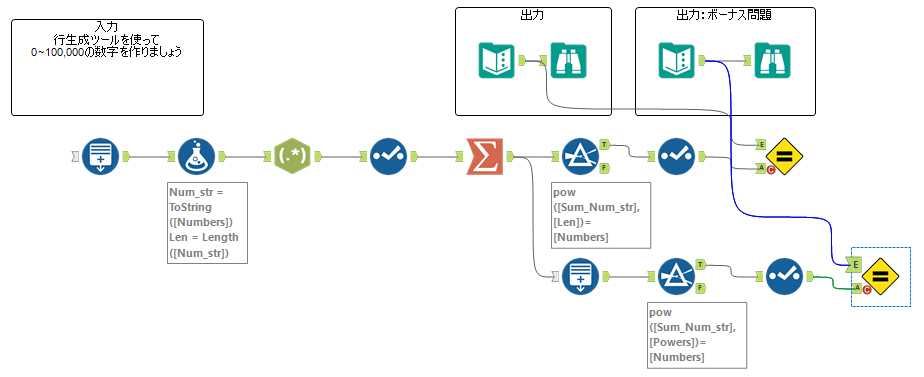
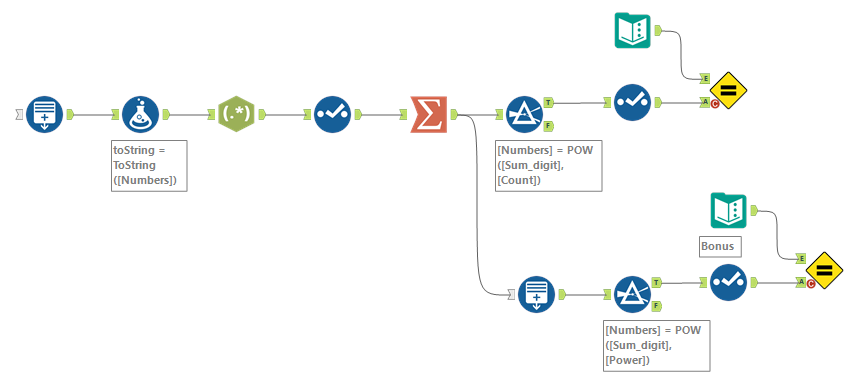
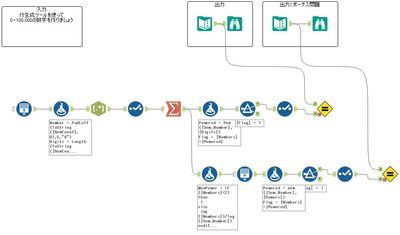
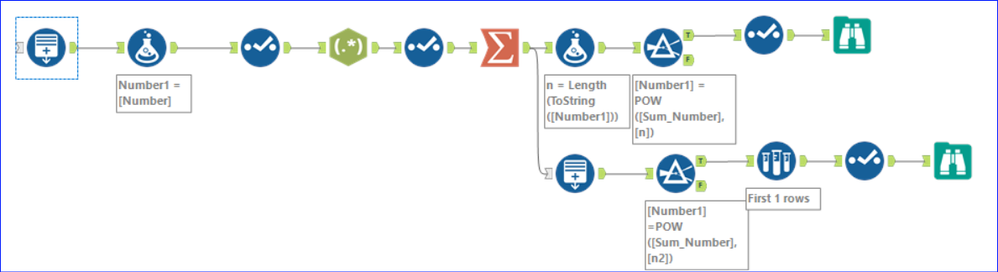
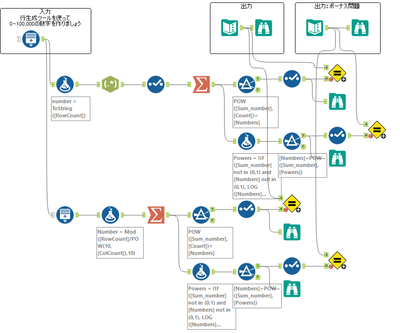
円周率πに敬意を表して、今週のあなたのタスクは、桁の合計の n 乗に等しい 100,000 以下の 13 個の数値をすべて見つけることです。たとえば、81 は 2 桁の数値であるため、n=2、(8+1)² = 81 となります。したがって、それは私たちが探しているカテゴリに当てはまります。

入力として、行生成ツールを使用して 0 ～ 100,000 の数値を生成します。

ボーナス問題: スキルを次のレベルに引き上げたい場合は、各桁の合計の n 乗に等しい 17 個の数字をすべて見つけてみましょう。例えば、これには 4,913 が該当します。 (4 + 9 + 1 + 3)⁴ = 83,521 であるため、最初のタスクには当てはまりませんが、(4 + 9 + 1 + 3)³ = 4,913 であるため、ボーナス問題では 正解となります。

もう少し手助けが必要ですか？　アカデミーにあるインタラクティブレッスンを見返してみてください：

・データの集計

・正規表現を作成する

健闘を祈ります！

[Tokimatsu]

数学を活用する回でしたね。

スポイラ

正規表現で各桁に分割するパターンと行生成で各桁に分解するパターンを作りました。対数はうろ覚えだったのでググって復習しました。

 

[AkimasaKajitani]

できました！

スポイラ

 

[Yoshiro_Fujimori]

回答します。

表題の元ネタはToy Storyの "To infinity and beyond!" ですかね。

スポイラ

Workflow

[smiyazawa]

できました！

スポイラ

スポイラ

[Qiu]

GWはウィークリーチャレンジをやりましょう。😁

スポイラ

[DaisukeTsuchiya]

周回遅れですが、できました。GWボケです。

スポイラ

[SNaka]

正規表現による分割を縦持ちするか横持ちするかで両方作ってみましたが、今回のパターンでは縦持ちの方がsumツールに繋げられるので楽ですね。一般論として、いくつに分割されるかわからないケースや、分割後のテキストから一部の情報のみ抽出して利用するケースなどを踏まえると、縦持ちの方が使いやすくファーストチョイスとすべきなのかもしれない気がしました。（自信はないですが。。）

[gawa]

@SNaka さん

おっしゃる通り、分割数が不明(動的)な場合には、行方向に分割するほうが、汎用性のあるWFになります！（分割後に元のレコードが特定できなくなるので、分割前にレコードIDで一意の番号振ることで、後々の処理が楽になります）