Blog
Visiones e ideas de las mentes más brillantes en el campo del análisis.- Suscribirse a un feed RSS
- Marcar como nuevo
- Marcar como leída
- Favorito
- Suscribir
- Página de impresión sencilla
- Notificar al moderador
- Suscribirse a un feed RSS
- Marcar como nuevo
- Marcar como leída
- Favorito
- Suscribir
- Página de impresión sencilla
- Notificar al moderador
Un modelo de ML con restricciones monotónicas es un tipo de modelo de aprendizaje automático (ML) que impone restricciones de monotonicidad a las variables de entrada. Monotonicidad significa que a medida que aumenta el valor de una variable, la salida del modelo siempre aumenta o siempre disminuye, si el resto de variables no cambian.
Estas restricciones son importantes porque pueden ayudar a mejorar la interpretabilidad del modelo al garantizar que el modelo se comporta de forma intuitiva y explicable. Por ejemplo, en algunas aplicaciones, es importante que las predicciones de un modelo aumenten o disminuyan a medida que aumentan determinadas características de entrada, como en la modelización del riesgo de crédito, en la que la probabilidad de impago debería aumentar a medida que aumenta el ratio deuda/ingresos (o debt-to-income) de un prestatario.
Además, los modelos con restricciones de monotonicidad pueden ser más robustos a los cambios en las variables y menos susceptibles de sufrir de sobreajuste u overfitting. Al obligar al modelo a comportarse de una determinada manera, también se reduce el riesgo de hacer predicciones poco razonables fuera del rango de los datos de entrenamiento, por lo que el modelo generaliza mejor.
En general, los modelos ML con restricciones monotónicas pueden proporcionar salvaguardas adicionales y mejor interpretabilidad que pueden ser importantes en determinadas aplicaciones.
Los sectores bancario y de seguros son grandes usuarios de modelos de ML que pueden necesitar restricciones monotónicas, con algunos ejemplos de casos de uso:
- Modelos de calificación crediticia: En los modelos de calificación crediticia, la probabilidad de que un prestatario deje de pagar un préstamo debería aumentar a medida que disminuye su calificación crediticia. Por lo tanto, puede ser importante imponer una restricción de monotonicidad en la variable de la puntuación de crédito para garantizar que el modelo se comporta de una manera intuitiva y explicable.
- Modelos de pricing de seguros: Los modelos de pricing de seguros suelen utilizar una serie de factores para determinar el perfil de riesgo de un asegurado, como la edad, el sexo o el historial de conducción. En algunos casos, ciertas variables deben presentar una relación monótona con la probabilidad de presentar un siniestro. Por ejemplo, en el seguro de automóvil, la probabilidad de sufrir un accidente aumenta a medida que aumenta el número de kilómetros recorridos.
- Modelos de detección de fraudes: Los modelos de detección de fraudes en el sector bancario suelen utilizar una serie de datos transaccionales y de comportamiento para identificar posibles casos de fraude. En algunos casos, ciertas variables pueden tener una relación monótona con la probabilidad de fraude, como por ejemplo, un aumento repentino de la frecuencia o el importe de las transacciones, que puede ser indicativo de actividad fraudulenta.
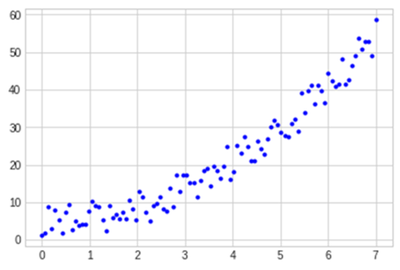
Pero, por lo general, los datos, representados gráficamente con respecto a una variable que debería tener un efecto monótono, mostrarán en realidad algo parecido a esto:
Esto se debe a que la realidad no es perfecta. Así que, en estos casos, es necesario poder imponer el efecto monotónico para algunas variables del modelo antes de que se apruebe para su uso en negocio.
Aunque las restricciones de monotonicidad pueden ser beneficiosas en muchos casos, también puede haber situaciones en las que aplicar la monotonicidad puede tener consecuencias no deseadas. Un ejemplo de un caso en el que la monotonicidad puede parecer una buena idea pero no serlo es en los modelos que implican interacciones entre variables. Por ejemplo, si consideramos un modelo que predice la satisfacción del cliente con un producto basándose en dos variables como el precio y la calidad. Se podría suponer que la satisfacción del cliente aumenta monotónicamente con la calidad, lo que significa que los productos de mayor calidad siempre conducen a una mayor satisfacción. Del mismo modo, se podría suponer que la satisfacción del cliente disminuye monotónicamente con el precio, lo que significa que los productos de menor precio siempre darán lugar a una mayor satisfacción. Sin embargo, en realidad, puede haber interacciones entre estas variables que hagan que las restricciones de monotonicidad sean menos efectivas. Por ejemplo, si el precio es demasiado bajo, los clientes pueden percibir que la calidad es baja, lo que conduce a una menor satisfacción. Por otra parte, si el precio es demasiado alto, los clientes pueden tener grandes expectativas de calidad y sentirse decepcionados si la calidad no cumple sus expectativas, lo que también conduce a una menor satisfacción. En este caso, la aplicación de restricciones de monotonicidad a cualquiera de las dos características por sí sola puede no captar las complejas interacciones entre precio y calidad y dar lugar a predicciones subóptimas.
Por lo tanto, es importante considerar cuidadosamente las relaciones entre las variables del modelo y sus objetivos generales antes de decidir aplicar restricciones de monotonicidad, y en cualquier caso, observar los efectos de las variables en todo su espectro antes de forzar este tipo de relaciones.
Hemos subido a la galería la nueva macro preparada para modelos de clasificación binaria. Es posible que publiquemos macros adicionales para problemas de clasificación multiclase o de regresión si hay interés en ello.
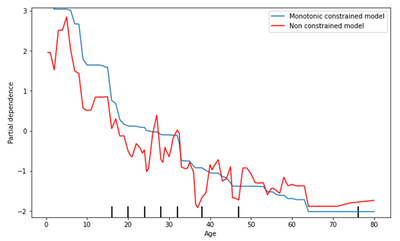
Además de la macro subida a la galería, hemos incluido dos flujos de trabajo en este post como ejemplos de cómo se puede utilizar la macro. Como conjunto de datos de demostración, hemos utilizado el conjunto de datos Titanic, que permite predecir la probabilidad de supervivencia de un pasajero basándose en su información demográfica. En este dataset, los pasajeros más jóvenes tienen más probabilidades de sobrevivir, por lo que hemos marcado la edad como una restricción monotónica decreciente. Podemos ver el efecto de tener esta restricción frente a no tenerla en la siguiente figura:
Aunque la tendencia general siga siendo la misma, con la restricción monótona siempre se da el caso de que los pasajeros más jóvenes tienen más probabilidades de sobrevivir, en igualdad de condiciones, lo que reduce el posible sobreajuste y hace que el modelo sea más fácil de explicar. Esto puede incluso dar lugar a un modelo mejor por su capacidad de generalizar mejor.
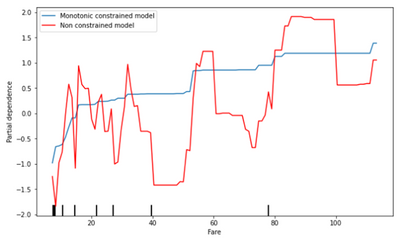
La segunda variable marcada como restricción es el precio que el pasajero pagó por el billete. Se da el caso de que los pasajeros de clases más altas tenían más posibilidades de sobrevivir, por lo que podemos ver el efecto de marcar el precio del billete para una restricción de monotonicidad creciente:
Esta macro ha sido probada con diferentes versiones de la librería Scikit-learn, por lo que debería funcionar en instalaciones Designer recién instaladas, pero funcionará mejor si la versión de esta librería Python es 1.0 o superior, especialmente con algunas variables que pueden tener un gráfico de dependencia parcial ausente en versiones inferiores de esta librería.
Y como siempre con los modelos de aprendizaje automático, por favor asegúrate de que entiendes los datos y el modelo y que un experto haya comprobado el modelo antes de usarlo en un escenario real.
¡Espero que esto sea útil para sus modelos!
Debe ser un usuario registrado para añadir un comentario aquí. Si ya está registrado, inicie sesión. Si todavía no está registrado, hágalo e inicie sesión.
-
20.4
1 -
2019.1
1 -
2019.4
3 -
2020.3
1 -
2021
1 -
2021.1
2 -
2021.2
1 -
2021.3
1 -
2021.4
1 -
2022.1
1 -
2022.3
2 -
2024.1
1 -
@AlteryxOSS
1 -
abril
1 -
abrir el archivo más reciente
1 -
abrir varias hojas
1 -
abrir varios archivos
1 -
Academia
1 -
ACE Program
1 -
activar licencias
1 -
Advanced Analytics
1 -
AED
2 -
agregar macros a Designer
1 -
agregar macros a la paleta de bloques en designer
1 -
agregar macros a la paleta de herramientas de designer
1 -
agregar macros a la paleta de herramientas en designer
1 -
agrupación de temas
2 -
AI
1 -
ALTER.NEXT
1 -
Alteryx
16 -
Alteryx 2020.1
1 -
Alteryx Analytics
2 -
Alteryx Analytics Hub
1 -
Alteryx automation
1 -
alteryx beta program
1 -
Alteryx Designer
4 -
Alteryx Excellence Awards
1 -
Alteryx Gallery
1 -
Alteryx intelligence suite
6 -
alteryx multi-threaded processing engine
1 -
alteryx open source
1 -
Alteryx public gallery
1 -
Alteryx Server
3 -
AlteryxLATAM
1 -
AML
3 -
AMP
1 -
AMP Engine
2 -
Analisis
1 -
Analitica
1 -
analytical apps
2 -
Analyticon
1 -
Analyticon 2021
1 -
Analytics
1 -
Analytics Hub
1 -
analítica
3 -
analítica de autoservicio
3 -
Análisis de Datos
1 -
análisis exploratorio
2 -
APA
3 -
aplicaciones analíticas
2 -
aprendizaje automática
1 -
aprendizaje automático
4 -
aprendizaje automático automatizado
1 -
aprendizaje automático de Alteryx
3 -
Artificial Intelligence
3 -
asociación
1 -
Assisted modeling
1 -
ateryx add-on
1 -
atualización
1 -
augmented intelligence
1 -
Auto Insights
1 -
Automation
1 -
Automatización
1 -
AutoML
1 -
badges
1 -
baja tipo de cambio
1 -
bajar archivos
1 -
base de conocimiento
1 -
Batch Macro
1 -
beta
1 -
biblioteca
1 -
Big Data
1 -
Big Data Analytics
1 -
big query
1 -
build features
1 -
buscar y reemplazar
1 -
Business Intelligence
1 -
Cadena de Suministro
1 -
Características nuevas
1 -
carga masiva
1 -
cargador
1 -
Certificación Alteryx Designer Core
1 -
certificación Core
5 -
cfo
3 -
chatbots
1 -
ChatGPT
1 -
Ciencia de datos
2 -
ciudadano científico de datos
1 -
clasificación de imágenes
2 -
Cloud
1 -
cluster de palabras
1 -
clusters de palabras
1 -
clusters de temas
1 -
comenzar Alteryx
1 -
Community
1 -
Compose
1 -
conector big query
1 -
conector google big query
1 -
conectores
1 -
conexión con API
1 -
configurar Alteryx
1 -
core certification
4 -
Core Certified
3 -
core exam
1 -
credly
1 -
Customer Advocacy
1 -
código abierto
1 -
Data
1 -
data health
1 -
Data Connection Manager
1 -
Database
1 -
Database Connection
1 -
datos
1 -
datos masivos
1 -
Deep Learning
1 -
descarga de archivos
1 -
descarga de la web
1 -
descarga tipo de cambio diario
1 -
Descargar
1 -
descargar archivo html
1 -
descargar macros
1 -
Designer
5 -
Desktop Automation
1 -
Digital
1 -
Digital Badge Program
1 -
download data
1 -
download tool
1 -
EDA
2 -
ejecutar flujos desde línea de comandos
1 -
EMEA
1 -
enero
1 -
Engine
1 -
entrada de datos
1 -
entrada dinámica
1 -
Error
1 -
error 3274
1 -
error al abrir Excel
1 -
error al abrir reportes de SAP
1 -
error en archivos de Excel
1 -
Etiquetas: Leer Excel
1 -
evento
1 -
eventos
16 -
Events
2 -
Excel
1 -
Excel Users
2 -
exceles
1 -
Expresiones Escritas
1 -
extracción de texto
1 -
extraer datos
2 -
feature engineering
3 -
feature type
1 -
Featuretools
1 -
Finanzas
5 -
flujos automatizados
1 -
flujos automáticos
1 -
FTP
1 -
Fuentes de Datos
1 -
galería Alteryx
1 -
galería pública
1 -
Gallery
1 -
generación de características
1 -
geoespacial
1 -
geospatial
1 -
Grand Prix
1 -
grupo de usuarios
1 -
grupos de palabras
2 -
grupos de temas
1 -
identificación de defectos
2 -
identificación de fallas
2 -
identificación de temas
2 -
identificación de tópicos
1 -
imagen a texto
1 -
información
1 -
ingeniería de características
4 -
iniciar sesión
1 -
Innovator
1 -
Inspire
4 -
Inspire EMEA
1 -
instalar Alteryx
1 -
instalar intelligence suite
1 -
instalar IS
1 -
instalar licencias
1 -
Instalar macros en Designer
1 -
Inteligencia artificial
3 -
inteligencia aumentada
1 -
Intelligence Suite
9 -
lanzamiento
1 -
LATAM
2 -
lectura de pdf
1 -
leer imágenes
1 -
leer pdf
1 -
leer un rango
1 -
licencia Alteryx
1 -
licencias alteryx
1 -
limpieza de datos
2 -
login
1 -
línea de comandos
1 -
Machine Learning
5 -
Macro
2 -
Macro batch
1 -
macro estándar
1 -
Macros
2 -
Map
1 -
maps
1 -
maps not showing
1 -
Marketing
1 -
marzo
1 -
mi equipo se murió
1 -
minería de texto
1 -
modelado asistido
2 -
modelado de temas
1 -
modelado de tópicos
2 -
modelado predictivo
3 -
modelo de clasificación entrenado
1 -
modelo de exportación
1 -
motor
1 -
motor de procesamiento paralelo
1 -
mover licencia
1 -
múltiples archivos de Excel
1 -
múltiples Excel
1 -
múltiples exceles
1 -
New release
2 -
News
1 -
NLP
2 -
no aparecen los mapas
1 -
no puedo abrir archivo de Excel
1 -
no puedo entrar
1 -
no se ve el mapa
1 -
no se ven los mapas
1 -
no tengo mapas
1 -
Noticias
1 -
noviembre
1 -
nube de palabras
2 -
nueva versión
3 -
OCR
3 -
octubre
1 -
On-demand
1 -
OpenAI
1 -
OSS
1 -
perfilado de datos
2 -
Performance
1 -
plantillas de pdf
1 -
PLN
2 -
prejudice
1 -
prejuicios
1 -
premios
1 -
Preparación de datos
2 -
preparar archivo html
1 -
preprocesamiento de texto
2 -
preview
1 -
primeros pasos Alteryx
1 -
procesamiento de lenguaje natural
2 -
procesamiento paralelo
1 -
programa Beta
1 -
Public Gallery
1 -
Python
2 -
reconocimiento de imágenes
2 -
reconocimiento de texto
2 -
Regex
2 -
Reports
1 -
Resultado
1 -
revocar licencia
1 -
rpa
1 -
Run Command
1 -
run workflows from command line
1 -
salud de los datos
1 -
segregación
2 -
según demanda
1 -
separación de imágenes
2 -
Server
1 -
SFTP
1 -
Snowflake
2 -
SSO
1 -
tableau public
1 -
Text Mining
1 -
texto no estructurado
1 -
texto semiestructurado
1 -
Tip de la Semana
1 -
tipo de cambio Banxico
1 -
tipo de cambio diario
1 -
tipos de características
1 -
Tips + Tricks
1 -
Tools
2 -
top colaboradores
3 -
Top Contributors
2 -
topic modeling
1 -
Transformación digital
2 -
Transformation
1 -
tricks
1 -
trucos
1 -
varios archivos de Excel
1 -
versión 2020.3
1 -
versión 2020.4
1 -
versión 2021.2
1 -
versión más reciente
1 -
VGI
1 -
Virtual Global Inspire
1 -
visión artificial
1 -
visualización de datos
2 -
Visualization
1 -
Webinar
7 -
webinars
4 -
Word cloud
1 -
Workflow
5 -
Writing Expressions
1
- « Anterior
- Siguiente »
-
Garabujo7 en: Nueva macro para entrenar modelos de ML con restri...
-
Garabujo7 en: Tip de la Semana (14) - Los contenedores
- BorjaR en: Tip de la Semana (13) - Macros por Lotes o Batch ...
-
anguiano en: Hay vida más allá de los dashboards - Introducción...
-
Garabujo7 en: Macro ChatGPT para resolver tareas comunes de Alte...
-
Garabujo7 en: Tip de la Semana(9) -¿Buscando la Velocidad? II-Ef...
-
mpost en: ¿Qué es Alteryx?
-
Garabujo7 en: Cómo deshacerse del error de metadatos no válidos ...
-
mpost en: TOP COLABORADORES - Q4 2021
-
FláviaB en: Alteryx Analytics Gallery se mudará a la Comunidad