Data Science
Machine learning & data science for beginners and experts alike.- Community
- :
- Community
- :
- Learn
- :
- Blogs
- :
- Data Science
- :
- Building a 'Return to Work' Timetable in Alteryx
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
Alteryx Community user @michalklofac recently posed an interesting question, trying to understand how Alteryx Designer could be used to optimise the use of office space as governments begin to start allowing people to return to work.
In this case, we’re going to demonstrate how it’s possible to build an employee timetable based on constraints such as the days in which your employees want to work in the office and when they want to work remotely, how many times they’d like to work in the office each week, whilst also thinking about office capacity, given employers are likely to have reduced office capacity given the need for social distancing to be maintained.
You can download the accompanying workflow here.
Let’s start by looking at the data required in order to solve this problem. Firstly, we need some data on your employees' desired working pattern, and really we need to answer three questions:
- Do they actually want to return to the office?
- If they do, how often do they want to be in the office each week?
- Again, if they do, are there any particular days when they cannot be in the office?
I decided to mock up some sample data (based on a company with capacity for 2 employees their office). I then transformed the data into the two formats shown below, one of which gives information on the days in which each employee is happy to be in the office, and another which indicates the minimum and maximum number of days each week they would like to spend in the office.
|
employee_number |
weekday |
|
128493 |
Tuesday |
|
128493 |
Wednesday |
|
128493 |
Thursday |
|
128493 |
Friday |
|
238492 |
Monday |
|
238492 |
Tuesday |
|
238492 |
Thursday |
|
238492 |
Friday |
|
294942 |
Monday |
|
294942 |
Tuesday |
|
294942 |
Wednesday |
|
294942 |
Thursday |
|
294942 |
Friday |
|
employee_number |
min |
max |
|
128493 |
1 |
3 |
|
238492 |
2 |
3 |
|
294942 |
5 |
5 |
We also need some data covering the maximum capacity of our office, with social distancing restrictions in place, this is our third input:
|
capacity |
|
2 |
Just these three inputs is all we require to build out our optimization model in Alteryx - let's do it!
So firstly, we need to think about our output, which may sound a bit odd, but it will allow us to get an understanding of what our first input needs to look like. In this case, we are looking to create an employee timetable, which, for every employee and day of the week, will flag whether they are allowed to attend the office or not.
We can pull two things out of the above statement, first of all, ‘for every employee and day of the week,’ these two items, together, form our ‘decision variables’ (the options we are choosing from). We can only have a single ‘decision variable’ field and therefore we must concatenate our ‘employee number’ and ‘weekday’ fields together, which can be done with a simple Formula tool (whenever you are doing concatenation, and working with the Optimization tool, I would recommend using the underscore _ character (due to the way the Cross Tab tool works, which is often required for building other inputs required for the Optimization tool).
The second thing we can pull out of this statement is ‘will flag whether they are allowed to attend the office or not.’ Therefore we are creating an outcome that is binary. The decision variable can either be selected, or not selected, it can’t be somewhere in between.
This detail allows us to create the ‘options’ anchor (‘o’ anchor) for our Optimization tool.
|
decision |
type |
coefficient |
|
128493_Tuesday |
B |
1 |
|
128493_Wednesday |
B |
1 |
|
128493_Thursday |
B |
1 |
|
128493_Friday |
B |
1 |
|
238492_Monday |
B |
1 |
|
238492_Tuesday |
B |
1 |
|
238492_Thursday |
B |
1 |
|
238492_Friday |
B |
1 |
|
238492_Monday |
B |
1 |
|
238492_Tuesday |
B |
1 |
|
238492_Wednesday |
B |
1 |
|
238492_Thursday |
B |
1 |
|
238492_Friday |
B |
1 |
With the ‘options’ input, a ‘coefficient’ field is also required. The coefficient field permits us to refine our optimisation by allowing people to specify ranked preferences.In our case, the coefficient field should be an arbitrary value against all rows, as we didn’t give our employees to specify any preference.
Given that we are performing a binary analysis, there is no need to specify upper and lower bounds for our value, as you may have seen in other blogs on optimization.
The second input to look at is the ‘b’ anchor for our Optimization tool, this is where we must specify the constraints to our problem, in our case we have two sets of constraints that we need to bring together. The first set of constraints is around our employees and how often they are happy to attend the office each week.
|
constraint |
dir |
rhs |
|
128493_min |
>= |
1 |
|
238492_min |
>= |
2 |
|
128493_max |
<= |
3 |
|
238492_max |
<= |
3 |
|
238492 |
== |
5 |
We must specify our min and max values on different rows, as different variables (in this case I’ve simply suffixed the employee number with ‘min’ and ‘max.’ For any individuals whereby the minimum and maximum values are the same we only need to give a single constraint.
The second set of constraints relates to our office capacity; we only have a maximum capacity but this capacity applies each day.
|
constraint |
dir |
rhs |
|
Monday |
<= |
2 |
|
Tuesday |
<= |
2 |
|
Wednesday |
<= |
2 |
|
Thursday |
<= |
2 |
|
Friday |
<= |
2 |
Depending on the size of your workforce, you may want to give minimum number of employees in the office each day (for example, to reduce energy waste caused by very few people being assigned to the office on a particular day), in which case, similarly to what we have done with the employee constraints, we may duplicate our variables and change the direction of our constraint.
The final thing we need to tell our optimisation model is how the selection of each of our decision variables contributes to each of our constraints. In order to do this, we can structure our data in two ways, either with our decision variables down our vertical axis and constraints across our horizontal axis (known in the Optimization tool as ‘Dense Matrix, variables in rows’), or with our constraints down our vertical axis and decision variables across our horizontal axis (known in the Optimization tool as ‘Dense Matrix, constraints in rows’). We are going to choose the former, for no other reason than my personal preference.
|
decision |
128493_min |
128493_max |
238492_min |
238492_max |
238492 |
|
128493_Tuesday |
1 |
1 |
|
|
|
|
128493_Wednesday |
1 |
1 |
|
|
|
|
128493_Thursday |
1 |
1 |
|
|
|
|
128493_Friday |
1 |
1 |
|
|
|
|
238492_Monday |
|
|
1 |
1 |
|
|
238492_Tuesday |
|
|
1 |
1 |
|
|
238492_Thursday |
|
|
1 |
1 |
|
|
238492_Friday |
|
|
1 |
1 |
|
|
238492_Monday |
|
|
|
|
1 |
|
238492_Tuesday |
|
|
|
|
1 |
|
238492_Wednesday |
|
|
|
|
1 |
|
238492_Thursday |
|
|
|
|
1 |
|
238492_Friday |
|
|
|
|
1 |
|
decision |
Monday |
Tuesday |
Wednesday |
Thursday |
Friday |
|
128493_Tuesday |
|
1 |
|
|
|
|
128493_Wednesday |
|
|
1 |
|
|
|
128493_Thursday |
|
|
|
1 |
|
|
128493_Friday |
|
|
|
|
1 |
|
238492_Monday |
1 |
|
|
|
|
|
238492_Tuesday |
|
1 |
|
|
|
|
238492_Thursday |
|
|
|
1 |
|
|
238492_Friday |
|
|
|
|
1 |
|
238492_Monday |
1 |
|
|
|
|
|
238492_Tuesday |
|
1 |
|
|
|
|
238492_Wednesday |
|
|
1 |
|
|
|
238492_Thursday |
|
|
|
1 |
|
|
238492_Friday |
|
|
|
|
1 |
The tables above are separated for illustrative purposes but they would be ‘joined’ together in Alteryx (remember the workflow is attached to this blog!), with just a single decision column and only one row per decision.
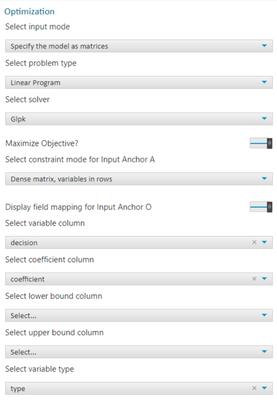
Once we have generated all of our inputs we can then pass them into our Optimization tool, there are some slight configuration changes that we need to make and I’ve shown these in the image below.
The first thing we need to control is the ‘Maximize or Minimize Objective' switch; in this case I’ve decided that I want to maximise the objective, which, in our case, will maximise attendance within our office without breaching our constraints. You could choose to minimise the objective, which in this case would give people the bare minimum amount of time they wish to spend in the office.
The other adjustments that we have to make to the default configuration are to change the ‘Constraint Mode’ to ‘Dense matrix, variables in rows’, and also map the different fields of our ‘Options’ or ‘O’ anchor.
We can now run our workflow, and the ‘S’ or ‘Solution’ anchor coming from our Optimization tool will contain a list of the selected decision variables, alongside the total objective value.
With some simple transformation steps applied, we can take this data we and build our timetable which we can share with our employees.
|
employee_number |
Mon |
Tue |
Wed |
Thu |
Fri |
Total Days |
|
128493 |
N |
N |
Y |
Y |
N |
2 |
|
238492 |
Y |
Y |
N |
N |
N |
3 |
|
294942 |
Y |
Y |
Y |
Y |
Y |
5 |
|
Total Employees |
2 |
2 |
2 |
2 |
2 |
|
It’s possible that you will get the response ‘Solution is undefined,’ this response means that you do not have the seating capacity in your office to meet the very minimum requested days specified by your employees, in which case, you’ll need to think carefully about whether it’s possible to increase the capacity in the office, or whether you can work with your employees to loosen the minimum desired requirements.
Important to note: Something I noticed when using the Optimization tool is that the order of values in your data matters. In this scenario, the order of values in the constraints list should match the order of fields created by the Cross Tab (which is alphabetical order), and this is why we have used a sort tool on the constraints list prior to passing it into the Optimization tool. Your decisions in both the ‘options’ input and ‘a’ input should also be in the same order.
Photo by Erik Odiin on Unsplash
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.