Data Science
Machine learning & data science for beginners and experts alike.- Community
- :
- Community
- :
- Learn
- :
- Blogs
- :
- Data Science
- :
- And For My Next Trick: An Introduction to Support ...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
Support Vector Machines (often abbreviated as SVMs) are supervised machine learning algorithms that find a boundary or line that effectively describes the training data, either giving the most possible separation between the boundary and the training data points on each side (classification) or by finding the line as close as possible to the largest number of training points (regression).
To understand SVMs, there are a few basic concepts we need to get a hold on first. To define basic SVM concepts, we will be looking at a basic binary classification problem. Once we get the basics down, we can move on to support vector regression and the kernel trick.
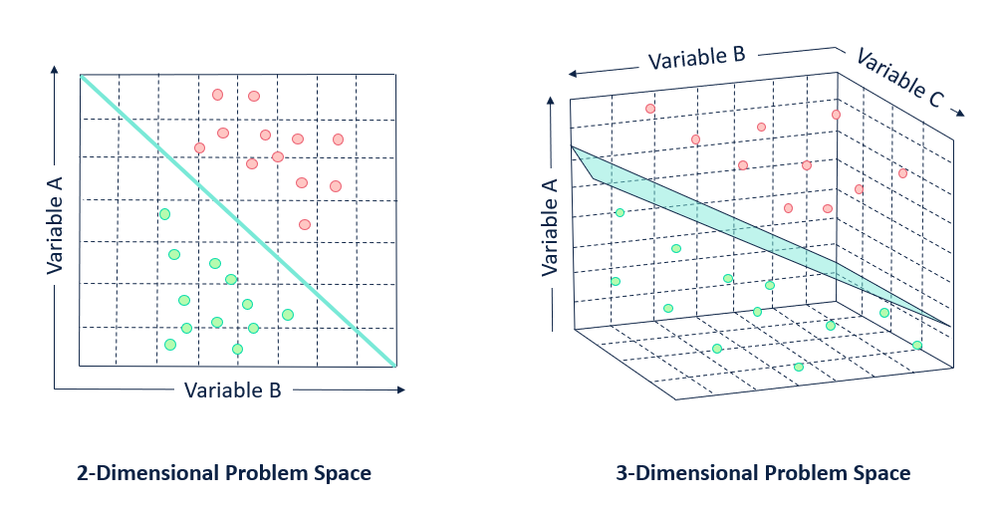
Variable Space
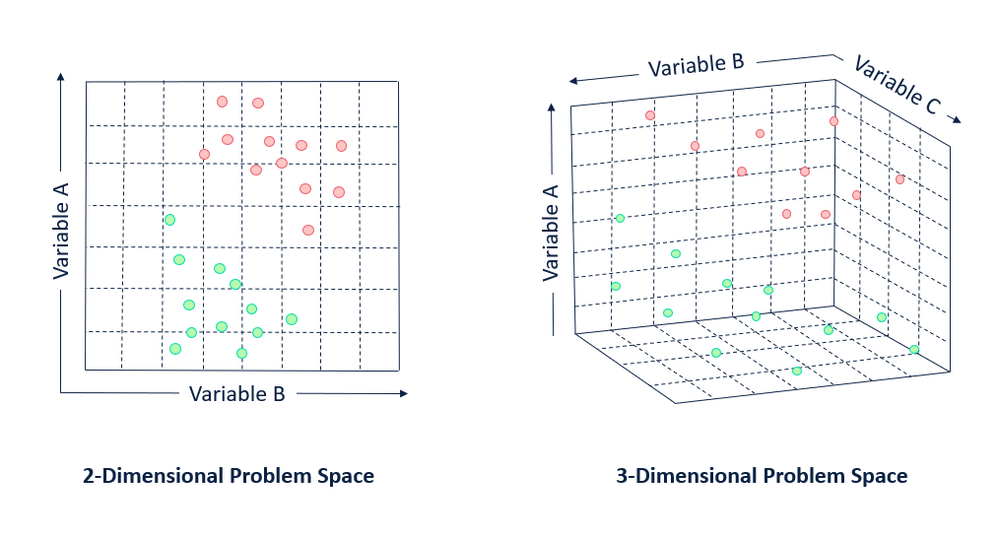
A support vector machine thinks about individual observations (rows) in a data set as points plotted in n-dimensional space, where n is the number of predictor variables you are using to describe your target variable.
For example, if you have three variables: A, B, and C, your points will be plotted in the corresponding three-dimensional space based on their values for each predictor variable.
 Decision Boundaries
Decision Boundaries
After determining where the observations in your data set exist in n-dimensional space, an SVM identifies a hyperplane called a decision boundary that separates your data. By definition, a hyperplane will always have one less dimension than the data space it is built in (e.g., if you are working in a three-dimensional space a hyperplane will have two dimensions, and if you are working in a two-dimensional space, your hyperplane will be a line).
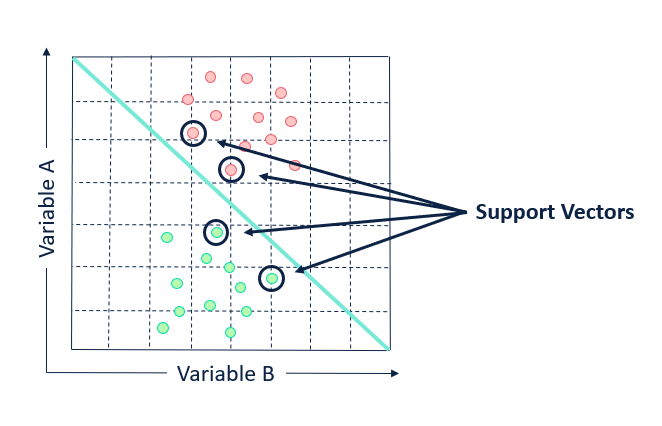
Support Vectors
An SVM attempts to identify an optimal decision boundary that will clearly separate the different target variable classifications. The decision boundary of an SVM is determined by support vectors. Support vectors points that are closest to the edge of each class and are the most difficult points to correctly classify.
In the eyes of an SVM, only the support vectors are important. If the support vector points were moved or withheld from the data set, the position of the dividing hyperplane would be altered. Moving or withholding points that are not support vectors will have no impact. The other, more generic data points can be (and are) ignored for determining the boundary.
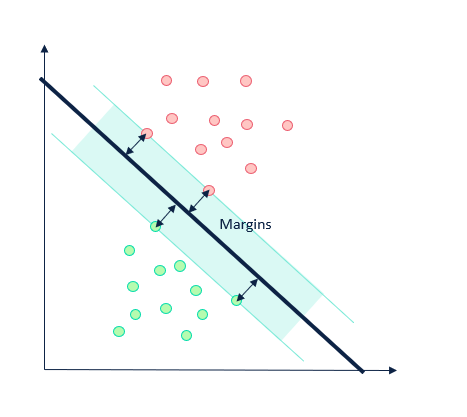
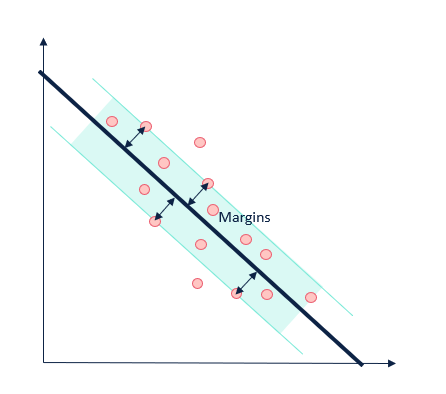
Margins
The distance between the hyperplane and the support vectors are called the margins. The goal of a support vector machine is to maximize the margins. This is how the model determines the optimal decision boundary.
The greater the width of the margins, the higher probability there is of correctly estimating the value of the included observations. Similarly, the further away from the hyperplane a data point is, the more confidence there is in the point being correctly identified.
To sum up a classification SVM (sometimes called a support vector classifier or SVC), the points on the edge of each classification group are used to determine a support boundary by maximizing the distance between those points and the dividing hyperplane. Not too tricky after all, right?
Support Vector Regression (SVR)
In many ways, an SVM approaches a regression problem in the opposite way it does a classification problem. Instead of trying to keep points outside of the margin, and create the widest margins possible, the SVM it will try to fit all the points within the margin of the hyperplane and minimize the number of points that fall outside of the margin.
If you'd like to know more about support vector regression, read the paper A tutorial on Support Vector Regression from Alex Smola and Bernhard Scholkopf.
The Kernel Trick
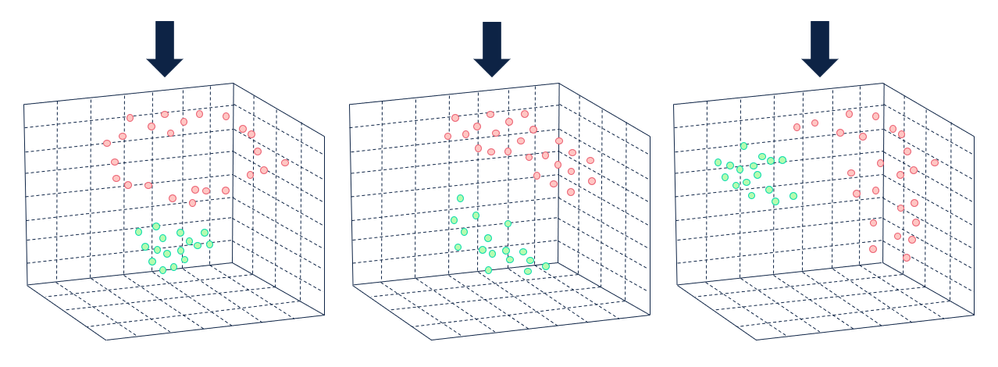
The illustrations thus far have been designed to take on a linear shape, but what happens when a data set is not linearly separable (separated by a straight line)?
This is where the kernel trick (also referred to as a kernel method or kernel function) comes into play. The kernel trick is a function that can be used to transform a data set into higher-dimensional space so that the data becomes linearly separable. The kernel trick effectively converts a non-separable problem into a separable one by increasing the number of dimensions in the problem space and mapping the data points to the new problem space.
The hyperplane that effectively separates the points in a higher-dimension problem space is mapped back to the original problem space, resulting in a non-linear solution.
If you'd prefer to see a live-action visualization, check this out:
What the kernel trick actually does is calculate pair-wise dot products, performing an implicit transformation without consuming extra memory and minimizing the effect on overall computation time. This allows SVM to effectively learn nonlinear boundaries by replacing dot products in SVM with the kernel function. This is the trick!
If you'd like to know more about the math and technical details of the kernel trick, read Eric Kim's Everything You Wanted to Know about the Kernel Trick (But Were Too Afraid to Ask).
Limitations
SVMs do not perform as well as other machine learning algorithms when the number of features (columns/predictor variables) is greater than the number of observations (rows). The training time for an SVM can also be very high, depending on the data set.
Strengths
SVMs are particularly effective in high-dimension spaces. There is also a wide variety of kernel functions to allow data to be separated in different ways. For more details, the blog post Why use SVM (a Yhat classic) gives a great overview of the many advantages of SVM.
Additional Resources
Support Vector Machine (SVM) – Fun and Easy Machine Learning is a great YouTube video that gives a high-level overview of how SVMs work.
An idiot’s guide to Support vector machines is slide deck from an MIT Artificial Intelligence course taught by Robert Berwick that gets into a little more of the theory behind SVMs.

A geographer by training and a data geek at heart, Sydney joined the Alteryx team as a Customer Support Engineer in 2017. She strongly believes that data and knowledge are most valuable when they can be clearly communicated and understood. She currently manages a team of data scientists that bring new innovations to the Alteryx Platform.
A geographer by training and a data geek at heart, Sydney joined the Alteryx team as a Customer Support Engineer in 2017. She strongly believes that data and knowledge are most valuable when they can be clearly communicated and understood. She currently manages a team of data scientists that bring new innovations to the Alteryx Platform.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.