Alteryx Designer Desktop Discussions
Find answers, ask questions, and share expertise about Alteryx Designer Desktop and Intelligence Suite.- Community
- :
- Community
- :
- Participate
- :
- Discussions
- :
- Designer Desktop
- :
- Re: Alteryx Odd Behavior
Alteryx Odd Behavior
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello everyone,
I have been pretty odd behavior from Alteryx on rounding numbers. At first I thought there was something wrong with the calculation, but apparently it is a defect. So I wanted to share this with the community to get feedback. I tested it on version 9.5, 10.5 and 11
so if you take an average of two numbers of (100, and 124.83) it will end up in 112.415. You can either do it manually or use function "average".
Now when you try to round the result to hundredth with round ( [X] , 0.01) it will end up at 112.41 instead of 112.42
Interesting part is if you code the number 112.415 manually then the result of rounding will be 112.42
It gets more interesting when you take the average of 100 and 224.83 instead of 124.83. The result of course is 162.415 and if we round it this time it will end up as 162.42. in other words "whole number" is affecting the decimal rounding which does not make sense to me.
I guess this should be probably a defect on the way that numbers are restored.
Fun fact: we found this issue on Halloween !
Solved! Go to Solution.
- Labels:
-
Common Use Cases
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Pasha_Maleknia This isn't a bug, but rather a limitation with how computers store and perform math operations on floating point numbers. Let's consider the number '1.025'. Due to limitations in precision with variable storage and the conversion to binary when this value is stored as a double the number actually gets stored as '1.024999999999999911182158029987476766109466552734375'. As such when rounded to 2 decimal places the number would round to 1.02 where you may expect it to round to 1.03. This is because computers can't store floating point values with exact precision, and some fractions are infinite in length (1/3 for example is 0.33333... repeating). Because of finite storage space if the value doesn't convert to an exact binary number or if it exceeds storage available for the variable it gets rounded. There is an excellent article here on the Community written by one of our developers explaining this in detail. I have included a link for that article below along with some third party article that go into more of the math behind the behavior.
Community Article:
Floating point numbers are surprisingly strange
Additional reading:
Why 0.1 Does Not Exist In Floating-Point
Inconsistent Rounding of Printed Floating-Point Numbers
Stack exchange discussion with a good simple explanation:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
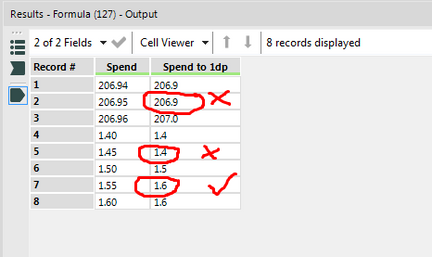
I'm having a similar issue with rounding. (Sample workflow attached and images pasted below)
There doesn't seem to be consistency in how decimal numbers ending in a 5 are rounded. In my test, two numbers were incorrectly rounded down and one was correctly rounded up. All us end-users expect to see "5 or more, raise the score. 4 or less, let it rest."
I understand the explanation, but my question is, regardless of the why, how do we get Alteryx to do what we expect it to do! :) Why is it that Excel can handle rounding? Has anyone discovered a workaround they'd be prepared to share?
Many thanks in advance


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@TeePee The rounding isn't inconsistent and it also isn't incorrect. As I previously stated this comes down to how fractional number are stored in binary by computers. For details on how this works I highly recommend reading the resources I linked to in my previous post.
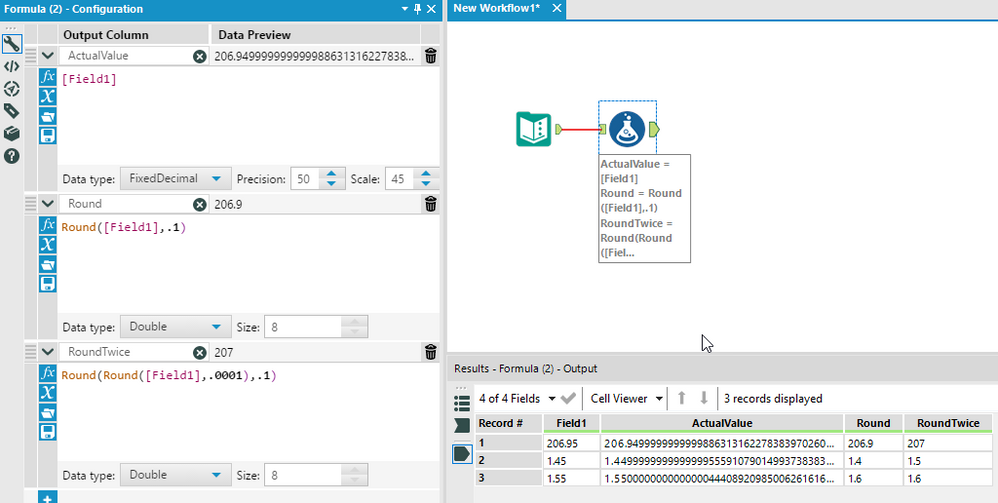
As for your specific example none of the rounding you performed is wrong. It just wasn't what you expected based on the input and because you aren't considering the real value of the number as stored by the computer. For example 206.95 when stored as a double in binary is actually '206.94999999999998863131622783839702606201171875' and when round at the first decimal place 206.94 becomes 206.9. 1.45 when stored as a double is actually '1.4499999999999999555910790149937383830547332763671875' which rounds as you saw to 1.4, and 1.55 when stored as a double is '1.5500000000000000444089209850062616169452667236328125' which rounds to 1.6. So the numbers are rounding exactly as you are telling them to in your formula, its just the that underlying number being used by the formula isn't what you expect because the number can't be stored exactly by the computer. As such the computer stores the number as the closest possible approximation that fits into the designated memory space. Sometimes this value is slight smaller than the actual number and sometimes it slightly larger.
To get the results you want/expect you need to be more precise with your rounding so that the stored value is greater than 206.950 when your do your final rounding. You can easily do this by rounding the number multiple time with multiple decimal places of precision prior to rounding at the single decimal place you want for your end result. See the screenshot below for an example.
If you are curious what a specific decimal value translates to when stored as a float or double by a computer you can use this link to find the actual value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
KevinP
While I did not read those articles, your explanations don't seem to address the bottom-line issue of this thread. Using Pasha_Maleknia's example above, the average of the numbers 100 and 124.83 rounded to two decimal places using mathematical rounding rules is 112.42. The Excel formula "=ROUND(AVERAGE(100,124.83),2)" returns the correct result 112.42; however, the Alteryx formula "ROUND(AVERAGE(100,124.83),0.01)" return the incorrect result of 112.41. It doesn't matter why Alteryx returns what it returns -- it only matters that Alteryx is returning the wrong value.
If Microsoft can get Excel to return the correct result, why can't Alteryx?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
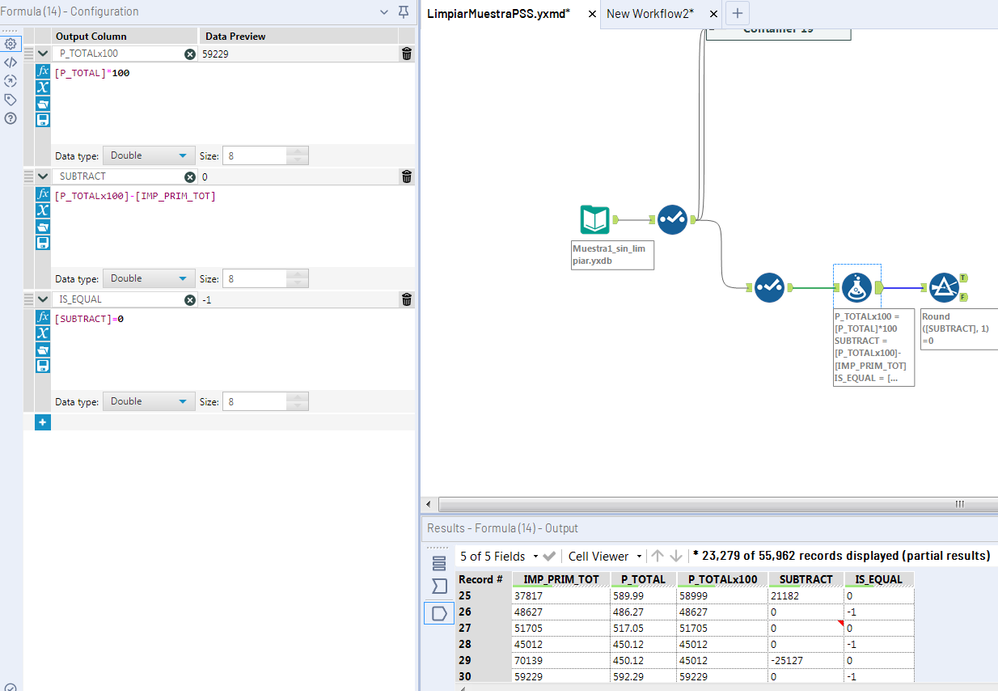
Another example here.
We have two fields, 'IMP_PRIM_TOT' and 'P_TOTAL'. They are both prices of a service, but IMP_PRIM_TOT would count '517.05€' as '51705' and P_TOTAL would count it as '517.05'. About half the times they are the same, and I am very interested in being able to check this with Alteryx.
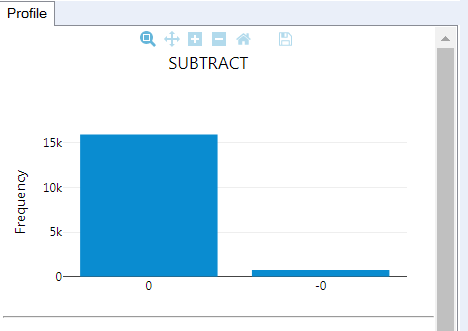
But it is not that easy. If I get 517.05 multiplied by 100 and subtracted to 51705, sometimes I get 0, but other times I get 'close to zero' and Alteryx see a difference that is not there.
Wrong values can be identified by the red dot, with a ''the display value was rounded to 6 decimal places for clarity" message, explaining why 0 is not 0.
Adding a filter at the end with Round(value, 1) gives us the number or miscalculations. In this case 2380 out of 16684 (15%).
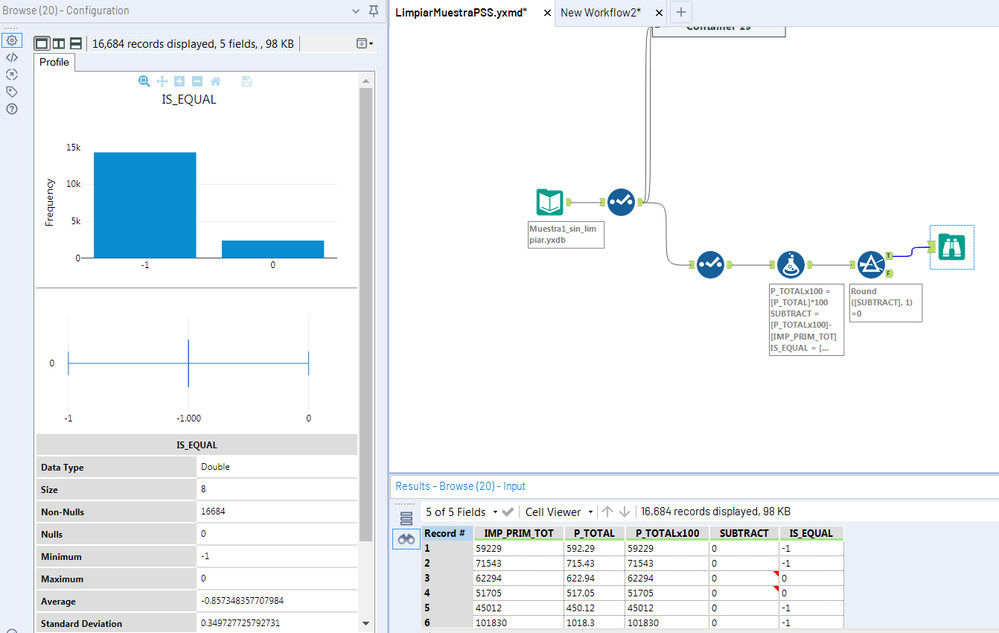
Also, it is not reproductible. If you pick the wrong cases, move them to other workflow and run it, you will not get the error in all of them. And in a small sample you will get no errors.
Big bug here. It is the result of a multiplication, and it happens randomly.
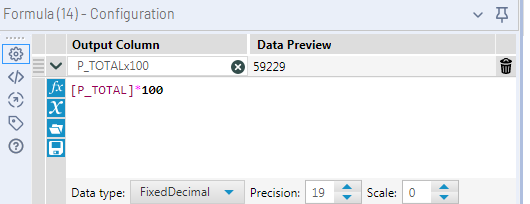
The solution I found for this situation was to change the type to FixedDecimal with 0 decimals.
You will still have to deal with '0' versus '-0' though
Keep this in mind when you are comparing numeric values.
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have been having a lot of issues with rounding. These are errors that we cannot afford to have as the workflows we built are used to audit billed amounts and must match the way our billing system calculates prorations. Initially we tried the round functions and then the round(round functions, but in the end we decided to manually round. For those that need Alteryx to round exactly as you intend on a calculated number I highly recommend a manual formula.
Example;
We bill a monthly rate of 717.21. However, in the month of March the contract came to an end mid month so we only want to bill 13 days.
so we have the first calculation of 717.21/31 = 23.135806 (we go to 6 decimals to match our billing system).
the second calculation is 23.135806 * 13 = 300.765478
Now comes the fun part, we take 300.765478 and Parse the data to reflect 300.76
*RegEx is (.*\.\d{2})
we also Parse the same number to pull out the 3rd decimal digit. so in this case I want to pull the '5' out 300.765478
*RegEx is \d*\.\d{2}(\d{1})\d*
Then we simply use a formula tool to determine if the 3rd digit is >= 5 and if so we add .01 so in this case we would have an ending result of 300.77
example of formula tool:
if [3rd decimal place] >= 5 then ([300.76] + .01) else [300.76] endif
We have had great success with this method applied to millions of different calculations over the last few weeks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Coming late to the party.
I've just run in to this issue as well.
I am unhappy with the response that 'floating point is hard'.
To solve this issue in my workflow dealing with financial data, I resorted to using the Python tool, in order to use Pandas to calculate the amount correctly.
The Python, for those who may wish to do this as well, is:
from ayx import Package
from ayx import Alteryx
import pandas as pd
data_to_manipulate = Alteryx.read("#1")
data_to_manipulate.column_that_needs_dividing = data_to_manipulate.column_that_needs_dividing.div(100)
Alteryx.write(data_to_manipulate, 1)
If you want to round your number, you can use this
data_to_manipulate.column_that_needs_dividing = data_to_manipulate.column_that_needs_dividing.div(100).round(2)
as the 5th line
The results that I got from this were as I expected them to be.
Alteryx: 19/100 = 0.189999997615814
Pandas: 19/100 = 0.19
Alteryx is a product that we pay for, Pandas is made available for free, and one of them has solved this issue.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know this is an older post, but I wanted to share the solution with those who've run into this issue for rounding in the past. https://community.alteryx.com/t5/Alteryx-Designer-Desktop-Discussions/Macro-for-rounding-Hint-Altery...
-
AAH
1 -
AAH Welcome
2 -
Academy
24 -
ADAPT
82 -
Add column
1 -
Administration
20 -
Adobe
174 -
Advanced Analytics
1 -
Advent of Code
5 -
Alias Manager
69 -
Alteryx
1 -
Alteryx 2020.1
3 -
Alteryx Academy
3 -
Alteryx Analytics
1 -
Alteryx Analytics Hub
2 -
Alteryx Community Introduction - MSA student at CSUF
1 -
Alteryx Connect
1 -
Alteryx Designer
44 -
Alteryx Engine
1 -
Alteryx Gallery
1 -
Alteryx Hub
1 -
alteryx open source
1 -
Alteryx Post response
1 -
Alteryx Practice
134 -
Alteryx team
1 -
Alteryx Tools
1 -
AlteryxForGood
1 -
Amazon s3
136 -
AMP Engine
187 -
ANALYSTE INNOVATEUR
1 -
Analytic App Support
1 -
Analytic Apps
17 -
Analytic Apps ACT
1 -
Analytics
2 -
Analyzer
17 -
Announcement
4 -
API
1,037 -
App
1 -
App Builder
42 -
Append Fields
1 -
Apps
1,165 -
Archiving process
1 -
ARIMA
1 -
Assigning metadata to CSV
1 -
Authentication
4 -
Automatic Update
1 -
Automating
3 -
Banking
1 -
Base64Encoding
1 -
Basic Table Reporting
1 -
Batch Macro
1,266 -
Beginner
1 -
Behavior Analysis
216 -
Best Practices
2,405 -
BI + Analytics + Data Science
1 -
Book Worm
2 -
Bug
619 -
Bugs & Issues
2 -
Calgary
58 -
CASS
45 -
Cat Person
1 -
Category Documentation
1 -
Category Input Output
2 -
Certification
4 -
Chained App
233 -
Challenge
7 -
Charting
1 -
Clients
3 -
Clustering
1 -
Common Use Cases
3,379 -
Communications
1 -
Community
188 -
Computer Vision
44 -
Concatenate
1 -
Conditional Column
1 -
Conditional statement
1 -
CONNECT AND SOLVE
1 -
Connecting
6 -
Connectors
1,174 -
Content Management
8 -
Contest
6 -
Conversation Starter
17 -
copy
1 -
COVID-19
4 -
Create a new spreadsheet by using exising data set
1 -
Credential Management
3 -
Curious*Little
1 -
Custom Formula Function
1 -
Custom Tools
1,713 -
Dash Board Creation
1 -
Data Analyse
1 -
Data Analysis
2 -
Data Analytics
1 -
Data Challenge
83 -
Data Cleansing
4 -
Data Connection
1 -
Data Investigation
3,046 -
Data Load
1 -
Data Science
38 -
Database Connection
1,892 -
Database Connections
5 -
Datasets
4,563 -
Date
3 -
Date and Time
3 -
date format
2 -
Date selection
2 -
Date Time
2,874 -
Dateformat
1 -
dates
1 -
datetimeparse
2 -
Defect
2 -
Demographic Analysis
172 -
Designer
1 -
Designer Cloud
471 -
Designer Integration
60 -
Developer
3,633 -
Developer Tools
2,907 -
Discussion
2 -
Documentation
449 -
Dog Person
4 -
Download
902 -
Duplicates rows
1 -
Duplicating rows
1 -
Dynamic
1 -
Dynamic Input
1 -
Dynamic Name
1 -
Dynamic Processing
2,525 -
dynamic replace
1 -
dynamically create tables for input files
1 -
Dynamically select column from excel
1 -
Email
740 -
Email Notification
1 -
Email Tool
2 -
Embed
1 -
embedded
1 -
Engine
129 -
Enhancement
3 -
Enhancements
2 -
Error Message
1,969 -
Error Messages
6 -
ETS
1 -
Events
176 -
Excel
1 -
Excel dynamically merge
1 -
Excel Macro
1 -
Excel Users
1 -
Explorer
2 -
Expression
1,690 -
extract data
1 -
Feature Request
1 -
Filter
1 -
filter join
1 -
Financial Services
1 -
Foodie
2 -
Formula
2 -
formula or filter
1 -
Formula Tool
4 -
Formulas
2 -
Fun
4 -
Fuzzy Match
613 -
Fuzzy Matching
1 -
Gallery
586 -
General
93 -
General Suggestion
1 -
Generate Row and Multi-Row Formulas
1 -
Generate Rows
1 -
Getting Started
1 -
Google Analytics
140 -
grouping
1 -
Guidelines
11 -
Hello Everyone !
2 -
Help
4,097 -
How do I colour fields in a row based on a value in another column
1 -
How-To
1 -
Hub 20.4
2 -
I am new to Alteryx.
1 -
identifier
1 -
In Database
852 -
In-Database
1 -
Input
3,704 -
Input data
2 -
Inserting New Rows
1 -
Install
3 -
Installation
305 -
Interface
2 -
Interface Tools
1,641 -
Introduction
5 -
Iterative Macro
948 -
Jira connector
1 -
Join
1,732 -
knowledge base
1 -
Licenses
1 -
Licensing
210 -
List Runner
1 -
Loaders
12 -
Loaders SDK
1 -
Location Optimizer
52 -
Lookup
1 -
Machine Learning
230 -
Macro
2 -
Macros
2,493 -
Mapping
1 -
Marketo
12 -
Marketplace
4 -
matching
1 -
Merging
1 -
MongoDB
66 -
Multiple variable creation
1 -
MultiRowFormula
1 -
Need assistance
1 -
need help :How find a specific string in the all the column of excel and return that clmn
1 -
Need help on Formula Tool
1 -
network
1 -
News
1 -
None of your Business
1 -
Numeric values not appearing
1 -
ODBC
1 -
Off-Topic
14 -
Office of Finance
1 -
Oil & Gas
1 -
Optimization
645 -
Output
4,491 -
Output Data
1 -
package
1 -
Parse
2,094 -
Pattern Matching
1 -
People Person
6 -
percentiles
1 -
Power BI
197 -
practice exercises
1 -
Predictive
2 -
Predictive Analysis
818 -
Predictive Analytics
1 -
Preparation
4,622 -
Prescriptive Analytics
185 -
Publish
229 -
Publishing
2 -
Python
727 -
Qlik
35 -
quartiles
1 -
query editor
1 -
Question
18 -
Questions
1 -
R Tool
452 -
refresh issue
1 -
RegEx
2,102 -
Remove column
1 -
Reporting
2,107 -
Resource
15 -
RestAPI
1 -
Role Management
3 -
Run Command
500 -
Run Workflows
10 -
Runtime
1 -
Salesforce
242 -
Sampling
1 -
Schedule Workflows
3 -
Scheduler
371 -
Scientist
1 -
Search
3 -
Search Feedback
20 -
Server
523 -
Settings
756 -
Setup & Configuration
47 -
Sharepoint
463 -
Sharing
2 -
Sharing & Reuse
1 -
Snowflake
1 -
Spatial
1 -
Spatial Analysis
556 -
Student
9 -
Styling Issue
1 -
Subtotal
1 -
System Administration
1 -
Tableau
461 -
Tables
1 -
Technology
1 -
Text Mining
409 -
Thumbnail
1 -
Thursday Thought
10 -
Time Series
397 -
Time Series Forecasting
1 -
Tips and Tricks
3,776 -
Tool Improvement
1 -
Topic of Interest
40 -
Transformation
3,202 -
Transforming
3 -
Transpose
1 -
Truncating number from a string
1 -
Twitter
24 -
Udacity
85 -
Unique
2 -
Unsure on approach
1 -
Update
1 -
Updates
2 -
Upgrades
1 -
URL
1 -
Use Cases
1 -
User Interface
21 -
User Management
4 -
Video
2 -
VideoID
1 -
Vlookup
1 -
Weekly Challenge
1 -
Weibull Distribution Weibull.Dist
1 -
Word count
1 -
Workflow
8,437 -
Workflows
1 -
YearFrac
1 -
YouTube
1 -
YTD and QTD
1
- « Previous
- Next »